Teorema: caracterización de los espacios conexos mediante conjuntos abiertos y cerrados (clopen)
Un espacio topológico \( X \) se denomina conexo si y solo si los únicos subconjuntos de \( X \) que son simultáneamente abiertos y cerrados (es decir, clopen) son el propio \( X \) y el conjunto vacío \( \emptyset \).
En términos equivalentes, un espacio topológico es conexo cuando los únicos subconjuntos clopen son los triviales: todo el espacio o el conjunto vacío.
Esto significa que no existen subconjuntos propios no vacíos de \( X \) que sean, a la vez, abiertos y cerrados.
El teorema establece un criterio fundamental para determinar la conexión topológica de un espacio sin recurrir a conceptos más avanzados como la conexión por caminos.
Explicación
En topología, un subconjunto que es a la vez abierto y cerrado separa el espacio en dos subconjuntos abiertos, disjuntos y no vacíos.
Si existe un conjunto clopen no trivial, es decir, distinto de \( X \) y de \( \emptyset \), entonces el espacio puede escribirse como la unión de dos abiertos disjuntos y no vacíos. En este caso, el espacio es no conexo o disconexo.
Por el contrario, si los únicos conjuntos clopen de \( X \) son \( X \) y \( \emptyset \), no existe una separación del espacio en abiertos disjuntos no vacíos, y por tanto \( X \) es un espacio conexo.
Observación. En cualquier espacio topológico, tanto el conjunto total \( X \) como el conjunto vacío \( \emptyset \) son siempre abiertos y cerrados.
Ejemplo 1: un espacio finito disconexo
Sea \( X = \{ a, b, c, d \} \) con la topología \( T \) definida por los conjuntos abiertos \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).
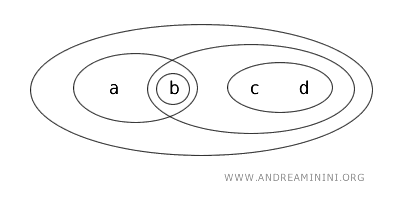
En este caso, el subconjunto \( \{ a, b \} \) es clopen, ya que cumple ambas propiedades:
- Es abierto porque figura explícitamente entre los abiertos de la topología \( T \).
- Es cerrado porque su complemento \( X \setminus \{ a, b \} = \{ c, d \} \) también es abierto en \( T \).
Por tanto, el espacio topológico \( (X, T) \) es disconexo, puesto que contiene un subconjunto propio no vacío que es clopen.
La existencia de un único conjunto clopen no trivial es suficiente para concluir que un espacio es disconexo.
En efecto, la presencia de un subconjunto clopen distinto de \( X \) y \( \emptyset \) muestra que el espacio puede expresarse como la unión de dos abiertos disjuntos y no vacíos, \( \{ a, b \} \) y \( \{ c, d \} \). En consecuencia, no se cumple la condición de conexión topológica.
Ejemplo 2: los números reales
Consideremos el conjunto de los números reales \( \mathbb{R} \) provisto de la topología usual, generada por los intervalos abiertos \( (a, b) \).
En esta topología, los intervalos \( (a, b) \) son conjuntos abiertos pero no cerrados, mientras que los intervalos \( [a, b] \) son cerrados pero no abiertos.
Los únicos subconjuntos de \( \mathbb{R} \) que son a la vez abiertos y cerrados son \( \mathbb{R} \) y \( \emptyset \).
Por tanto, \( \mathbb{R} \) con la topología usual es un espacio conexo.
Ejemplo 3: un subespacio disconexo de \( \mathbb{R} \)
Consideremos el subespacio \( X = (0,1) \cup (2,3) \subset \mathbb{R} \), provisto de la topología subespacio inducida por la topología usual de \( \mathbb{R} \).
En este caso, los intervalos \( (0,1) \) y \( (2,3) \) son abiertos y cerrados en \( X \), porque el complemento de cada uno dentro de \( X \) es el otro intervalo. Más precisamente:
- El complemento de \( (0,1) \) en \( X \) es \( (2,3) \), que es abierto en \( X \).
- El complemento de \( (2,3) \) en \( X \) es \( (0,1) \), que también es abierto en \( X \).
Por tanto, ambos subconjuntos son clopen.
Como existen subconjuntos no triviales que son simultáneamente abiertos y cerrados, el subespacio \( X \) es disconexo.
Esta falta de conexión se debe a que \( X \) puede expresarse como la unión de dos abiertos disjuntos y no vacíos, \( (0,1) \) y \( (2,3) \), que juntos cubren todo el espacio.