Conexidad mediante una intersección común
Sean \( C_1, C_2, \dots, C_n \subset X \) una colección de subconjuntos conexos de un espacio topológico \( X \) que comparten al menos un punto en común: \[ \bigcap_{i=1}^n C_i \neq \varnothing . \] En estas condiciones, la unión \( \bigcup_{i=1}^n C_i \) es un conjunto conexo.
De forma intuitiva, siempre que dos o más conjuntos conexos tengan al menos un punto en común, al unirlos se obtiene un conjunto que sigue siendo conexo.
Este resultado depende de manera esencial de la hipótesis de que todos los conjuntos comparten al menos un punto.
Nota. La condición \( \bigcap_{i=1}^n C_i \neq \varnothing \) es suficiente para garantizar la conexidad de la unión \( \bigcup_{i=1}^n C_i \), pero no es una condición necesaria. En efecto, una unión de conjuntos conexos puede seguir siendo conexa incluso cuando no existe un punto común a todos ellos. Esto sucede, por ejemplo, cuando los conjuntos se intersectan de forma encadenada.
Un ejemplo concreto
Consideremos los siguientes subconjuntos de \( \mathbb{R}^2 \):
- \( C_1 \): el segmento horizontal que va de \( (-1,0) \) a \( (1,0) \)
- \( C_2 \): el segmento vertical que va de \( (0,-1) \) a \( (0,1) \)
- \( C_3 \): el segmento diagonal que une \( (-1,-1) \) con \( (1,1) \)
Cada uno de estos conjuntos es conexo.
Además, todos contienen el punto \( (0,0) \). En efecto:
\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]
Por lo tanto, la intersección común no es vacía:
\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]
En consecuencia, según el criterio de conexidad, su unión es un conjunto conexo:
\[ C_1 \cup C_2 \cup C_3 \]
Los tres segmentos concurren en un mismo punto central, lo que garantiza que la unión sea conexa.
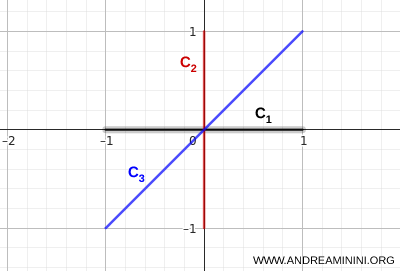
Desde cualquier punto de uno de los segmentos es posible llegar a cualquier otro punto desplazándose únicamente a través de puntos que pertenecen a la unión.
Nota. Existen otros criterios de conexidad que no exigen que todos los conjuntos \( C_i \) compartan un punto común. Por ejemplo, si los conjuntos \( C_i \) son conexos y se intersectan de forma encadenada, es decir, si \( C_i \cap C_{i+1} \neq \varnothing \), entonces su unión \( \bigcup_i C_i \) es conexa incluso cuando \( \bigcap_i C_i = \varnothing \). Sin embargo, esta condición tampoco es necesaria, ya que la unión puede seguir siendo conexa incluso cuando algunos pares consecutivos son disjuntos, siempre que otros conjuntos de la familia actúen como puentes. Un ejemplo claro es el de tres segmentos que forman un triángulo. Aunque su intersección total es vacía, \( \bigcap_i C_i = \varnothing \), la unión sigue siendo conexa.
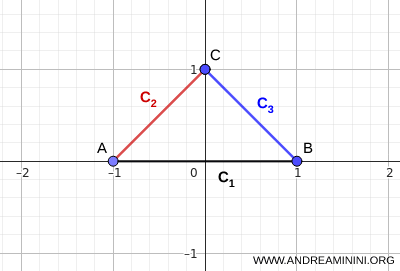
Este ejemplo muestra con claridad que la intersección en cadena es suficiente para garantizar la conexidad de la unión.
Demostración
Sea \( X \) un espacio topológico y sea \( \{C_i\}_{i \in I} \) una familia de subconjuntos conexos de \( X \) cuya intersección común no es vacía:
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
Supongamos, por reducción al absurdo, que la unión
\[ C = \bigcup_{i \in I} C_i \]
no es conexa.
Si \( C \) no es conexa, entonces existen dos abiertos \( U \) y \( V \) que constituyen una separación de \( C \), es decir:
- \( U \cap C \neq \varnothing \)
- \( V \cap C \neq \varnothing \)
- \( (U \cap C) \cap (V \cap C) = \varnothing \)
- \( C = (U \cap C) \cup (V \cap C) \)
Por hipótesis, existe un punto \( x \) que pertenece a todos los conjuntos \( C_i \):
\[ x \in \bigcap_{i \in I} C_i \]
Este punto común debe pertenecer a \( U \) o a \( V \), pero no a ambos. Supongamos, sin pérdida de generalidad, que
\[ x \in U \quad \text{y} \quad x \notin V \]
Como cada \( C_i \subset C \), se tiene:
\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]
Los conjuntos \( C_i \cap U \) y \( C_i \cap V \) son abiertos en la topología inducida sobre \( C_i \), son disjuntos y su unión es todo \( C_i \). Dado que \( C_i \) es conexo, uno de ellos debe ser vacío.
Por tanto, cada \( C_i \) está contenido por completo en uno de los abiertos:
\[ C_i \subset U \quad \text{o bien} \quad C_i \subset V \]
Como \( x \in C_i \) y \( x \in U \), no puede ocurrir que \( C_i \subset V \).
Se deduce entonces que
\[ C_i \subset U \quad \text{para todo } i \in I \]
En consecuencia,
\[ \bigcup_{i \in I} C_i \subset U \]
lo cual contradice la hipótesis de que \( V \cap C \neq \varnothing \).
Esta contradicción demuestra que la suposición inicial es falsa. Por lo tanto, la unión \( \bigcup_{i \in I} C_i \) es un conjunto conexo.
Y así sucesivamente.