Topología

La topología es una rama de las matemáticas que estudia las propiedades de los espacios que permanecen invariantes bajo deformaciones continuas, como estirar, doblar o retorcer, siempre que el objeto no se rompa ni se adhiera.

Desde esta perspectiva, la topología se interesa por aquellas propiedades geométricas que se conservan cuando una transformación es continua.

Estas propiedades solo pueden cambiar mediante operaciones discontinuas, por ejemplo al rasgar una parte del espacio o al unir dos regiones distintas.

Un ejemplo clásico es el de la esfera y el cubo, que son topológicamente equivalentes, ya que uno puede deformarse de manera continua en el otro sin necesidad de romper ni pegar.

Por el contrario, una esfera y un toro no son topológicamente equivalentes, porque para transformar uno en el otro sería necesario crear o eliminar un agujero, lo que inevitablemente implica romper o pegar.

En otras palabras, la topología se centra en cómo los espacios están organizados y conectados, más que en medidas precisas como la distancia, el tamaño o la forma.

Dentro del marco topológico, conceptos como la longitud, el área, el volumen o la medida angular dejan de ser relevantes. Lo que importa son las características cualitativas de las figuras y la posibilidad de transformarlas unas en otras mediante deformaciones continuas.

Este enfoque incluye, por ejemplo, la conexidad, la compacidad, el número de agujeros de un objeto y otras propiedades globales de un espacio.

La topología introduce el concepto de espacio topológico, y sus transformaciones fundamentales son los homeomorfismos, es decir, aplicaciones continuas e invertibles que deforman un espacio conservando su estructura topológica.

Por esta razón, la topología suele describirse como la «geometría de la lámina de goma»: los objetos se imaginan como si estuvieran hechos de un material elástico que puede estirarse, doblarse o comprimirse, pero no romperse ni pegarse. Se trata de un área esencial y profundamente unificadora dentro de las matemáticas modernas.

Historia

El desarrollo de la topología se inició en el siglo XVIII.

Sus raíces se remontan al problema de los Siete Puentes de Königsberg de Leonhard Euler, que introdujo conceptos fundamentales sobre conectividad y teoría de redes.

Este problema planteó cuestiones fundamentales acerca de las propiedades de los espacios, sentando las bases para el campo de la topología.

El problema de los Siete Puentes: En una isla fluvial, hay siete puentes. Partiendo de cualquier punto, ¿qué ruta permite cruzar cada puente exactamente una vez? Es crucial que no puedas cruzar el mismo puente más de una vez.

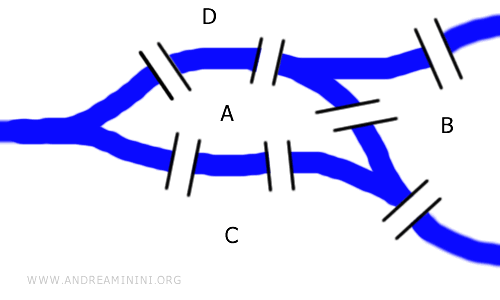
Este desafío no requiere conocimiento de distancias o longitudes de puentes; es esencialmente un problema topológico que también se puede representar usando grafos. El grafo mostrado aquí es topológicamente equivalente a la disposición original de los puentes.

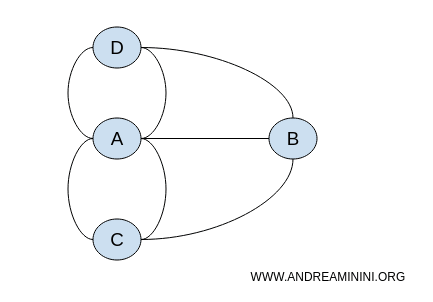
Las posiciones específicas de los nodos en el grafo no importan. Lo importante son las conexiones entre los nodos. Así, el problema podría representarse con un número infinito de grafos diferentes pero topológicamente equivalentes.

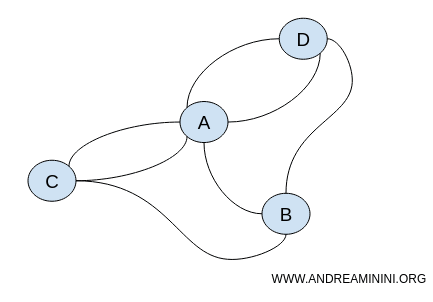
Ambos grafos mantienen las mismas propiedades topológicas, como la continuidad y las conexiones.

Euler se percató de que el problema de los Siete Puentes de Königsberg, aunque geométrico, no dependía de la medición de tamaños.

Mostró que el desafío era esencialmente sobre la posición y demostró que era irresoluble, dando origen al concepto de "geometría de posición".

Durante el siglo XIX, matemáticos como Carl Friedrich Gauss, August Ferdinand Möbius, Johann Listing, Bernhard Riemann y Felix Klein profundizaron en las propiedades de las formas y superficies, avanzando nuestro entendimiento de las propiedades topológicas.

Nota: Johann Listing fue quien acuñó el término "topología" en 1847, aunque solo se generalizó en la comunidad científica varias décadas después.

En el siglo XIX, la geometría de posición encontró aplicaciones prácticas en áreas como el análisis de redes eléctricas, gracias a Gustav Kirchhoff.

M ás adelante, Henri Poincaré, a finales del siglo XIX y principios del XX, hizo contribuciones significativas a la geometría de posición a través de su trabajo en la topología algebraica.

En el siglo XX, la topología se diversificó en subcampos especializados como la topología algebraica y la topología general, con importantes aportes de matemáticos como Felix Hausdorff, Cantor y Brouwer, en el ámbito de las matemáticas abstractas.

Actualmente, la topología es un campo esencial de las matemáticas dedicado al estudio de propiedades que se conservan bajo transformaciones continuas.

La topología abarca ahora varias subdisciplinas, cada una centrada en diferentes aspectos de los espacios topológicos, incluyendo la topología algebraica, la topología diferencial, la topología general y la topología geométrica.

En conjunto, la topología se puede considerar desde una perspectiva más amplia como el estudio general de las formas y, teóricamente, como una disciplina matemática abstracta.

A pesar de su naturaleza abstracta, los conceptos topológicos son aplicables a una variedad de problemas reales en campos tan diversos como la economía, la ingeniería y las ciencias.

Espacios topológicos

Un espacio topológico es un conjunto X dotado de una estructura T conocida como "topología", que proporciona un marco para comprender conceptos abstractos como la continuidad, la proximidad y los límites de manera más amplia y general que la geometría tradicional o el análisis matemático.

$$ (X,T) $$

Ejemplo: Un clásico ejemplo de espacio topológico es la línea de números reales \( \mathbb{R} \), que con su topología estándar define un conjunto como abierto si incluye un intervalo alrededor de cada punto. Este arreglo facilita la exploración de conceptos como la continuidad y los límites desde una perspectiva topológica.

Homeomorfismos

Un homeomorfismo es una transformación continua y biyectiva entre dos espacios topológicos, cuya inversa también es continua, conservando así propiedades topológicas fundamentales.

Dos espacios se consideran esencialmente iguales en topología si existe un homeomorfismo entre ellos.

Ejemplo: Transformar una taza de café en una rosquilla es un clásico ejemplo de homeomorfismo. Ambos objetos tienen un solo agujero y pueden ser transformados el uno en el otro mediante deformaciones continuas sin cortar ni pegar, conservando así sus características topológicas esenciales.

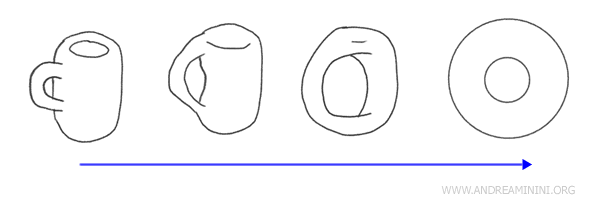
Geometría versus topología

Mientras que la geometría y la topología son campos distintos, están interrelacionados, cada uno enfocándose en diferentes aspectos de los espacios matemáticos.

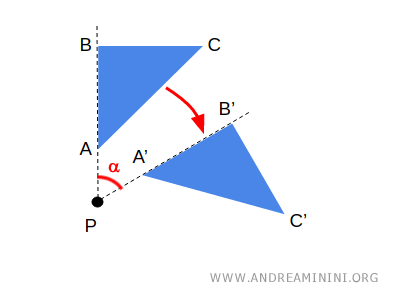
• Geometría se ocupa de propiedades relacionadas con distancias, ángulos y mediciones, enfocándose en figuras concretas y sus relaciones espaciales. Un ejemplo es la rotación de una figura, una transformación geométrica que preserva las distancias.
  

  La geometría euclidiana es la forma más conocida, pero las geometrías no euclidianas exploran las implicaciones de modificar o negar el quinto postulado de Euclides (el postulado de las paralelas).

• Topología se centra en propiedades que se mantienen a pesar de que el espacio sufra transformaciones continuas como estiramientos o compresiones, sin rasgar ni pegar. Aborda aspectos cualitativos como la continuidad, la conectividad y la flexibilidad inherente de las formas. Por ejemplo, transformar un cubo en una esfera mantiene la conectividad entre puntos y la continuidad general, característica de una transformación topológica.
  

  Ejemplo: Un cubo de arcilla puede ser remodelado en una esfera mediante compresión, manteniendo su continuidad y conectividad sin añadir ni quitar material. Esto ilustra un homeomorfismo, un tipo fundamental de transformación topológica.
  

A pesar de sus diferencias, los campos de la topología y la geometría están estrechamente vinculados, con la topología considerada a menudo como una generalización de la geometría.

Topología amplía el alcance de la investigación para incluir propiedades más abstractas de los espacios, a diferencia del enfoque más rígido de la geometría.

Ramas de la topología

Las aplicaciones de la topología abarcan diversas áreas de las matemáticas y la ciencia, cada rama enfocándose en aspectos únicos de los espacios topológicos.

• Topología en geometría: Aquí, el foco está en el estudio de propiedades que se conservan a través de transformaciones como estiramientos, contracciones y doblajes, sin rasgar ni pegar. Esta rama, conocida como topología geométrica, estudia propiedades como la continuidad, la conectividad, la compacidad y los límites sin considerar la distancia.
• Topología general (o Topología de conjuntos de puntos): Esta rama estudia los espacios topológicos de manera amplia y abstracta, enfocándose en propiedades como conjuntos abiertos y cerrados, continuidad, compacidad y conectividad, así como en espacios métricos y espacios de funciones.
• Topología algebraica: La topología algebraica utiliza herramientas algebraicas para estudiar los espacios topológicos, vinculando estructuras algebraicas a estos espacios para entender mejor sus propiedades.
• Topología diferencial: Esta rama utiliza cálculo diferencial para explorar las propiedades y estructuras de los espacios topológicos, particularmente aquellos que se asemejan localmente al espacio euclidiano, permitiendo la definición de conceptos como la tangencia y la diferenciabilidad.
• Topología aplicada: La topología aplicada se refiere al uso de métodos topológicos en aplicaciones prácticas fuera de las matemáticas puras, como en análisis de datos, ciencia de redes, ingeniería y biología computacional.

Cada rama de la topología tiene su propio enfoque, metodologías y aplicaciones, reflejando la versatilidad y la amplia aplicabilidad de los conceptos topológicos.