Puntos de acumulación en topología

Un punto $x$ en un espacio topológico $X$ es un punto de acumulación de un subconjunto $A \subseteq X$ si toda vecindad de $x$ intersecta al conjunto $A$ en al menos un punto distinto de $x$.

Es decir, en cualquier vecindad de $x$, siempre existe al menos un punto de $A$ que no coincide con $x$.

En otras palabras, $x$ es un punto de acumulación si la intersección de toda vecindad $U$ de $x$ con el subconjunto $A$ es no vacía.

$$ U \cap A \not = \emptyset $$

Un punto de acumulación no tiene por qué pertenecer al conjunto $A$; puede ser un punto externo.

En el caso del espacio topológico real $\mathbb{R}$, la noción de punto de acumulación resulta especialmente intuitiva. Sobre una recta, un punto $x$ es de acumulación para un subconjunto $A$ si cualquier vecindad de $x$, es decir, un intervalo del tipo $(x-\epsilon, x+\epsilon)$, contiene al menos un punto de $A$ distinto de $x\}.
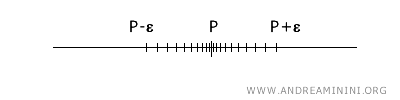
ilustración de un punto de acumulación sobre la recta real
La definición topológica de punto de acumulación extiende este concepto al espacio \(n$-dimensional $\mathbb{R}^n$: un punto $x$ será de acumulación para un conjunto $A$ si toda vecindad de $x$ lo intersecta en algún punto que no sea el propio $x$. Esta generalización, sin embargo, puede resultar menos intuitiva fuera de una dimensión.

Ejemplos prácticos
Observaciones

Ejemplos prácticos

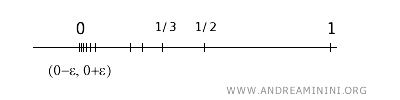
Consideremos el conjunto $A$ como subconjunto de $\mathbb{R}$ con la topología usual.

$$ A = \left\{ \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Este conjunto incluye los puntos $ \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots $, es decir, $\{1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots \}$.

Para determinar si $0$ es un punto de acumulación de $A$, consideremos una vecindad abierta cualquiera de $0$.

Toda vecindad de $0$ contiene un intervalo abierto $(a, b)$ tal que $a < 0 < b$.

Dado que $\frac{1}{n}$ converge a $0$ cuando $n$ tiende a infinito, siempre existe algún $\frac{1}{n}$ dentro del intervalo $(a, b)$, para $n$ suficientemente grande.

Por tanto, cualquier vecindad de $0$ contiene puntos de $A$ distintos de $0$.

En consecuencia, $0$ es un punto de acumulación del conjunto $A$.

representación de un punto de acumulación

Ejemplo 2

Veamos ahora el conjunto $B$, también considerado como subconjunto de $\mathbb{R}$ con la topología estándar.

$$ B = \left\{ n + \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Este conjunto contiene los puntos $ 1 + 1, 2 + \frac{1}{2}, 3 + \frac{1}{3}, \ldots $, es decir, $\{2, 2.5, 3.333\ldots, \ldots \}$.

Analicemos el punto $1$.

Cualquier vecindad abierta de $1$ contendrá necesariamente un intervalo del tipo $(a, b)$, con $a < 1 < b$.

No obstante, todos los elementos de $B$ son mayores que $1$, y para que alguno pertenezca a $(a, b)$, se requiere que $n + \frac{1}{n}$ esté comprendido entre $a$ y $b$.

Como ningún punto de $B$ es menor que $1$, no es posible encontrar puntos de $B$ en vecindades que contengan a $1$.

Por lo tanto, $1$ no es un punto de acumulación del conjunto $B$.

Ejemplo 3

Consideremos el conjunto $(0, 1]$ como un subconjunto de $\mathbb{R}$ dotado de la topología usual.

Nos proponemos determinar cuáles son los puntos de acumulación del conjunto $(0, 1]$.

De acuerdo con la definición, un punto $x$ es de acumulación de $(0, 1]$ si toda vecindad de $x$ intersecta a $(0, 1]$ en al menos un punto distinto de $x$.

Puntos interiores de $(0,1]$
Sea $x \in (0, 1]$. Cualquier vecindad de $x$ contiene un intervalo abierto $(a, b)$ tal que $a < x < b$. Dado que $x$ pertenece al intervalo $(0, 1]$, dicha vecindad intersecta necesariamente a $(0, 1)$ en puntos distintos de $x$. En consecuencia, todo punto $x \in (0, 1]$ es un punto de acumulación de $(0, 1]$.
Puntos frontera de $(0,1]$
Analicemos ahora los extremos del intervalo: $0$ y $1$.
- Punto $0$: Aunque $0$ no pertenece al conjunto $(0, 1]$, cualquier vecindad suya contiene un intervalo del tipo $(a, b)$ con $a < 0 < b$, que incluye infinitos puntos positivos pertenecientes a $(0, 1]$. Por tanto, $0$ es un punto de acumulación de $(0, 1]$.

- Punto $1$: Como $1$ pertenece al conjunto, cualquier vecindad suya - por ejemplo, un intervalo abierto $(a, b)$ con $a < 1 < b$ - contiene infinitos puntos de $(0, 1)$, distintos de $1$. En consecuencia, $1$ también es un punto de acumulación de $(0, 1]$.
Puntos fuera de $[0, 1]$
Por completitud, consideremos ahora cualquier punto $x \notin [0, 1]$. Si $x < 0$ o $x > 1$, es posible encontrar una vecindad de $x$ que no intersecta al conjunto $(0, 1]$.
Por ejemplo, si $x < 0$, se puede tomar un intervalo abierto $(x - \epsilon, x + \epsilon)$ con $\epsilon$ lo suficientemente pequeño como para que no contenga puntos de $(0, 1]$. De modo análogo, si $x > 1$, existe un intervalo abierto centrado en $x$ completamente disjunto de $(0, 1]$. Por tanto, ningún punto fuera del intervalo cerrado $[0, 1]$ es punto de acumulación de $(0, 1]$.

En conclusión, los puntos de acumulación del conjunto $(0, 1]$ en el espacio topológico $\mathbb{R}$ con la topología usual son precisamente los elementos del intervalo cerrado $[0, 1]$.

Ejemplo 4

Determinemos ahora el conjunto de puntos de acumulación de $ A = (0, 1] $ en la topología del límite inferior sobre $ \mathbb{R} $.

La topología del límite inferior sobre $ \mathbb{R} $ se genera a partir de los intervalos de la forma $[a, b)$, con $ a < b $. En consecuencia, los abiertos de esta topología son uniones arbitrarias de tales intervalos.

Un punto $x$ es de acumulación de un conjunto $A$ si toda vecindad suya contiene al menos un punto de $A$ distinto del propio $x$.

Examinemos los distintos casos:

Para $x \in (0, 1)$
Cualquier vecindad de $x$ en esta topología es de la forma $[x, x + \epsilon)$, la cual contiene infinitos puntos de $A$. Por tanto, $x$ es punto de acumulación de $A$.
Para $x = 1$
Aunque la topología del límite inferior no tiene intervalos del tipo $(1 - \epsilon, 1]$, existen vecindades de la forma $[1 - \epsilon, 1)$ que contienen puntos de $A$. Por ello, $1$ también es punto de acumulación de $A$.
Para $x = 0$
Toda vecindad de $0$, del tipo $[0, 0 + \epsilon)$, intersecta a $A$ en infinitos puntos. En consecuencia, $0$ es punto de acumulación de $A$.
Para $x < 0$ o $x > 1$
En estos casos, no existen vecindades del tipo $[x, x + \epsilon)$ que intersecten a $A$, por lo que dichos puntos no pueden ser de acumulación.

En resumen, los puntos de acumulación del conjunto $ A = (0, 1] $ en la topología del límite inferior sobre $ \mathbb{R} $ coinciden exactamente con los elementos del intervalo cerrado $[0, 1]$.

Es decir, el conjunto de puntos de acumulación de $ A $ es $[0, 1]$.

Observaciones

A continuación se presentan algunas observaciones relevantes sobre los puntos de acumulación:

La clausura de un conjunto es la unión del conjunto con sus puntos de acumulación
La clausura de un subconjunto $A$ de un espacio topológico $X$ está dada por la unión de $A$ con el conjunto $A'$ de sus puntos de acumulación: $$ \text{Cl}(A) = A \cup A' $$ En otras palabras, $\text{Cl}(A)$ incluye todos los puntos de $A$ y todos aquellos puntos del espacio que son límites de sucesiones (o más generalmente, de filtros o redes) de elementos de $A$.
Una sucesión puede converger a un punto de acumulación
Si $ A $ es un subconjunto de $ X = \mathbb{R} $, dotado de la topología usual, y $ x $ es un punto de acumulación de $ A $, entonces existe una sucesión $ \{x_i\} \subseteq A \setminus \{x\} $ que converge a $ x $. Cabe señalar que el punto de acumulación no necesariamente pertenece al conjunto $ A $; de hecho, puede ser completamente exterior a él.
Unicidad del punto límite
En la topología estándar sobre $ \mathbb{R} $, el límite de una sucesión - cuando existe - es único. Sin embargo, esta propiedad no se preserva en todas las topologías: en espacios no hausdorff, por ejemplo, una misma sucesión puede converger a más de un punto. La unicidad del límite depende por tanto de las propiedades de separación del espacio topológico considerado.

Estas observaciones permiten comprender mejor el papel fundamental que desempeñan los puntos de acumulación en la estructura topológica de los conjuntos.