Conjuntos Cerrados

Un conjunto $ B $ dentro de un espacio topológico $ X $ se dice cerrado si, para cada elemento del complemento $ u \in X - B $, existe un entorno completamente contenido en el complemento $ X - B $.
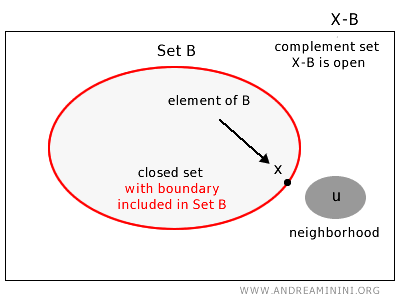
ejemplo de un conjunto cerrado

En otras palabras, un conjunto es cerrado si contiene todos sus puntos frontera.

De manera más rigurosa, un conjunto $ B $ en un espacio topológico $ X $ es cerrado si su complemento $ X - B $ es un conjunto abierto.

Nota: Esto implica que en $ B $ hay al menos un punto alrededor del cual no es posible encontrar un entorno completamente contenido en $ B $.

Un ejemplo práctico
El complemento de un conjunto cerrado
Ejemplo
Propiedades de los conjuntos cerrados
Ejemplo
Notas Adicionales

Un ejemplo práctico

Consideremos la recta real $ \mathbb{R} $ y un intervalo cerrado.

¿Qué es un intervalo cerrado? Un intervalo cerrado en $ \mathbb{R} $ es el conjunto de todos los puntos $ x $ que satisfacen $ a \leq x \leq b $, donde $ a $ y $ b $ son números reales con $ a < b $, e incluyendo ambos extremos.

Los intervalos cerrados se denotan como $[a,b]$, donde los corchetes indican que los extremos $ a $ y $ b $ pertenecen al conjunto.

Por ejemplo, el intervalo cerrado $[3,10]$ es un conjunto cerrado en la recta real $ \mathbb{R} $.

En este caso, el conjunto $ B $ está formado por todos los números comprendidos entre 3 y 10, incluyendo ambos extremos.

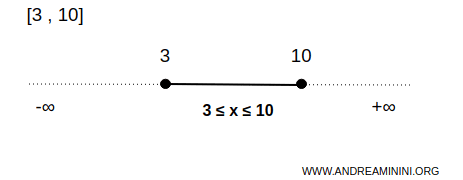
ejemplo de un intervalo cerrado

Esto significa que cualquier punto $ x $ que cumple $ 3 \leq x \leq 10 $ pertenece al conjunto, incluyendo los extremos $ x=3 $ y $ x=10 $.

Sin embargo, en este caso, no todos los puntos tienen un entorno completamente contenido dentro del intervalo $[3,10]$.

Por ejemplo, cualquier entorno del extremo inferior $ x=3 $ contendrá necesariamente puntos menores que 3, los cuales no están en el intervalo.

Nota: Incluso si se considerara un entorno infinitesimal, como $ 3 \pm 0.00000001 $, este no estaría completamente contenido en $[3,10]$, ya que $ 3 - 0.00000001 < 3 $. Lo mismo ocurre con el extremo superior $ x=10 $, donde tampoco existe un entorno completamente contenido en el intervalo.

Este es un ejemplo sencillo de un conjunto cerrado en una dimensión.

Otros ejemplos de conjuntos cerrados

La misma idea se puede extender al plano ($\mathbb{R}^2$).

Consideremos, por ejemplo, el conjunto de puntos de un disco de radio $ r=1 $ con centro en el origen $(0,0)$:

$$ x^2 + y^2 \leq 1 $$

Esta desigualdad describe el conjunto de todos los puntos cuya distancia al centro $(0,0)$ es menor o igual a 1, incluyendo tanto los puntos del interior del disco como los de la circunferencia.

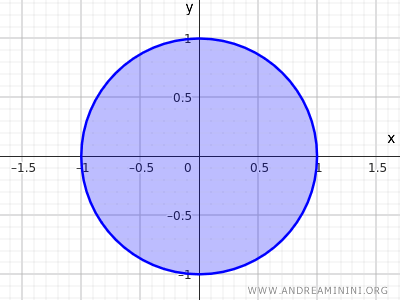
ejemplo de un conjunto cerrado en el espacio bidimensional

Este es otro ejemplo de conjunto cerrado.

Como se puede ver, los puntos sobre la circunferencia $ x^2 + y^2 = 1 $ no tienen entornos completamente contenidos dentro del disco cerrado.

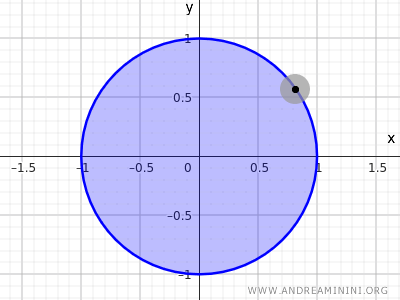
ejemplo de un conjunto cerrado

Nota: En topología, la circunferencia definida por la ecuación $ x^2 + y^2 = 1 $ no es ni un conjunto abierto ni cerrado en el espacio euclidiano $ \mathbb{R}^2 $, ya que solo contiene los puntos de la circunferencia y excluye el interior. En cambio, el conjunto definido por la desigualdad $ x^2 + y^2 \leq 1 $, que incluye tanto los puntos internos como los de la circunferencia, es un ejemplo de conjunto cerrado porque contiene todos sus puntos frontera.

Siguiendo la misma idea, el concepto de conjunto cerrado se puede extender al espacio tridimensional con una esfera sólida y al espacio $ n $-dimensional con una $ n $-esfera cerrada.

El complemento de un conjunto cerrado

En un espacio topológico $ X $, el complemento de un conjunto cerrado $ C $ es un conjunto abierto, denotado como $ X - C $.

Es decir, si $ C $ es un conjunto cerrado en $ X $, su complemento $ X - C $ será necesariamente un conjunto abierto.

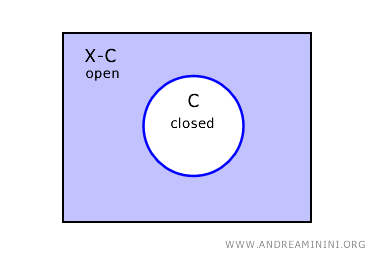
el complemento de un conjunto cerrado

Recíprocamente, si un conjunto $ U $ es abierto, su complemento $ X - U $ es un conjunto cerrado en $ X $.

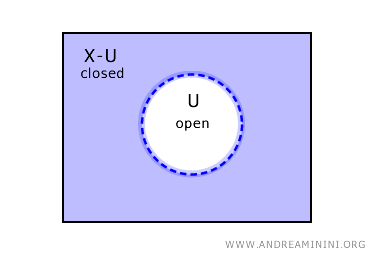
el complemento de un conjunto abierto

No obstante, estas no son las únicas posibilidades. En ciertos espacios topológicos pueden existir conjuntos que son simultáneamente abiertos y cerrados, así como conjuntos que no son ni abiertos ni cerrados.

En otras palabras, que un conjunto no sea cerrado no implica que sea abierto, y que no sea abierto no significa necesariamente que sea cerrado.

Ejemplo

Consideremos un espacio topológico $ (X, T) $, donde el conjunto $ X = \{a,b,c,d\} $ consta de cuatro elementos y la topología $ T $ está definida por los siguientes conjuntos abiertos:

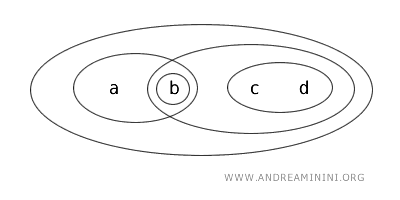
un ejemplo práctico

Los conjuntos abiertos en esta topología son: $ \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X $ y el conjunto vacío $ \varnothing $.

Analicemos algunos casos específicos:

El conjunto $ \{b\} $ es abierto, ya que está explícitamente definido como tal en la topología.
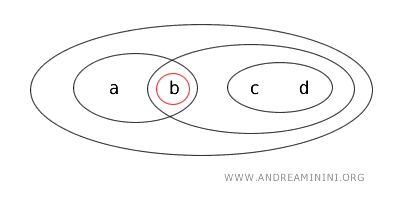
El conjunto $ \{a\} $ es cerrado porque su complemento es un conjunto abierto en la topología. En efecto, $ X - \{a\} = \{b,c,d\} $ es un conjunto abierto.
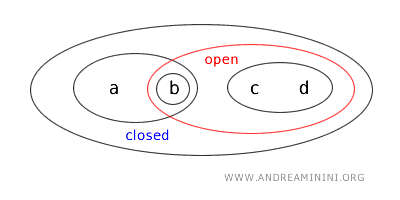
El conjunto $ \{a,b\} $ es tanto abierto como cerrado (clopen). Aunque en las topologías estándar sobre $ \mathbb{R} $ esto es poco común, en espacios más generales un conjunto puede ser simultáneamente abierto y cerrado si su complemento también es abierto. En este caso, $ \{a,b\} $ es abierto por definición de la topología y, además, su complemento $ X - \{a,b\} = \{c,d\} $ es abierto, por lo que también es cerrado.
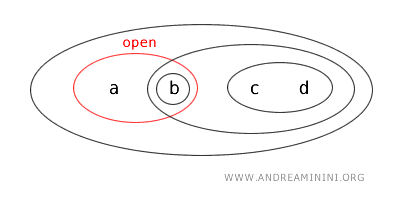
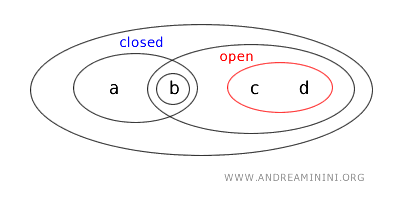
El conjunto $ \{b,c\} $ no es ni abierto ni cerrado. No aparece en la lista de conjuntos abiertos de la topología, y su complemento $ X - \{b,c\} = \{a,d\} $ tampoco es un conjunto abierto. Por lo tanto, no cumple con los criterios de apertura ni de clausura.

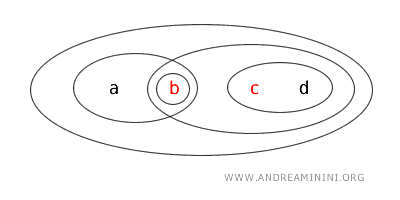
Este ejemplo ilustra que, en un espacio topológico, un conjunto puede ser abierto, cerrado, ambos a la vez (clopen) o ninguno de los dos.

Propiedades de los conjuntos cerrados

Un conjunto cerrado se define como el complemento de un conjunto abierto. Entre sus propiedades fundamentales se encuentran las siguientes:

El conjunto vacío ($\varnothing$) y el espacio total $ X $ son siempre conjuntos cerrados.
La intersección de cualquier colección (finita o infinita) de conjuntos cerrados es también un conjunto cerrado.
La unión de un número finito de conjuntos cerrados sigue siendo un conjunto cerrado.

Ejemplo

En la topología estándar del espacio euclidiano $ \mathbb{R}^n $, cualquier punto individual es un conjunto cerrado.

Si consideramos un punto $ n $ en la recta real ($ \mathbb{R}^1 $), su complemento es el conjunto de todos los puntos de $ \mathbb{R}^1 $ excepto $ n $.

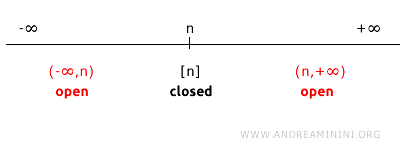
ejemplo

El complemento de $\{n\}$ es la unión de dos intervalos abiertos: $(-\infty, n) \cup (n, +\infty)$.

Dado que los intervalos $(-\infty, n)$ y $(n, +\infty)$ son abiertos en la topología estándar, su unión $(-\infty, n) \cup (n, +\infty)$ es también un conjunto abierto.

Por lo tanto, como el complemento de $\{n\}$ es abierto, concluimos que $\{n\}$ es un conjunto cerrado.

Sin embargo, no en todas las topologías los puntos individuales son necesariamente conjuntos cerrados. Esto depende de la estructura topológica del espacio.

Consideremos una topología sobre $ \mathbb{R} $ generada por los intervalos abiertos $ (n, n+1) $, para cada número entero $ n $. En esta topología, los puntos individuales $ n $ no son conjuntos cerrados porque no pueden expresarse como el complemento de un conjunto abierto.
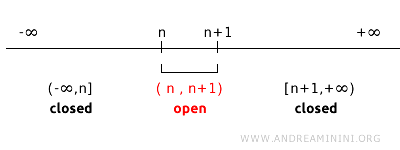
ejemplo
Por ejemplo, los conjuntos $ (1,2) $ y $ (2,3) $ son abiertos en esta topología. El complemento del conjunto abierto $ (1,2) $ es el conjunto $ (-\infty, 1] \cup [2, +\infty) $, mientras que el complemento del conjunto abierto $ (2,3) $ es $ (-\infty, 2] \cup [3, +\infty) $.

En esta topología, no es posible encontrar un conjunto abierto cuyo complemento sea exactamente $\{2\}$. De manera general, para cualquier conjunto abierto de la forma $ (n, n+1) $, su complemento es una unión de intervalos cerrados $ (-\infty, n] \cup [n+1, +\infty) $. Como resultado, en esta topología los puntos individuales $ n $ no son conjuntos cerrados, lo que demuestra que la noción de conjunto cerrado depende de la topología del espacio.

Notas Adicionales

Algunas observaciones relevantes:

Conjuntos Cerrados y Puntos de Acumulación
Un punto de acumulación de un conjunto es aquel en cuyo entorno arbitrariamente pequeño siempre hay al menos otro punto del conjunto. Esta propiedad caracteriza a los conjuntos cerrados, ya que un conjunto es cerrado si contiene todos sus puntos de acumulación.

Ejemplo: Consideremos el intervalo cerrado $[0,1]$ en la recta real. Este conjunto contiene todos sus puntos de acumulación.

Por ejemplo, el punto $0.5$ dentro de $[0,1]$ tiene cualquier entorno abierto que contenga infinitos puntos del intervalo, lo que confirma que $0.5$ es un punto de acumulación.
ejemplo de 0.5 como punto de acumulación en el intervalo cerrado [0,1]

Lo mismo ocurre con los extremos del intervalo. Por ejemplo, el punto $0$ es un punto de acumulación de $[0,1]$ porque cualquier entorno suyo contiene puntos del intervalo, como $0.1, 0.01, 0.001$, etc.
los extremos del intervalo cerrado [0,1] son puntos de acumulación
Así, todos los puntos de $[0,1]$ son puntos de acumulación del conjunto.

Un conjunto $ A $ es cerrado si y solo si $ A = \overline{A} $
En un espacio topológico, un conjunto $ A $ es cerrado si es igual a su cierre, es decir, si $ A = \overline{A} $. El cierre de $ A $, denotado $ \overline{A} $, está compuesto por todos los puntos de $ A $ junto con sus puntos de acumulación. Por definición, si un conjunto $ A $ contiene todos sus puntos de acumulación, entonces es un conjunto cerrado.

Y así sucesivamente.