Topología de conjuntos abiertos
Una topología T sobre un conjunto abierto X es una colección de subconjuntos de X considerados "abiertos" que cumple con las siguientes propiedades:
- El conjunto vacío Ø y el propio conjunto X se consideran abiertos por definición.
- La unión e intersección de cualquier número finito de conjuntos abiertos también son consideradas abiertas.
En otras palabras, la colección T debe incluir únicamente subconjuntos de X que se consideran "abiertos" y es cerrada bajo las operaciones de unión e intersección.
Donde una colección de conjuntos es un conjunto cuyos elementos son conjuntos o subconjuntos.
En estos casos, el conjunto X y la topología T constituyen un espacio topológico, a menudo denotado como el par (X,T).
Nota: Por simplicidad, a menudo se dice que X es un espacio topológico. Sin embargo, es importante recordar que un espacio topológico consta de dos elementos: la topología T (colección de subconjuntos) y el conjunto X.
¿Por qué se considera siempre al conjunto vacío como un conjunto abierto?
El conjunto vacío se considera abierto por definición en cada espacio topológico.
Esta convención es una parte fundamental de las definiciones de topología y asegura que las propiedades y axiomas de la topología sean consistentes y completos.
Un ejemplo práctico
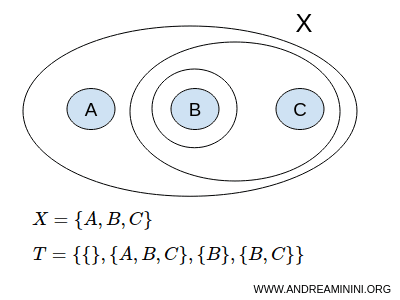
Consideremos un conjunto X que consta de tres elementos: A, B y C.
$$ X = \{ A,B,C \} $$
Una topología T podría estar formada por los subconjuntos { }, {A,B,C}, {B}, {B,C}.
$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \} \} $$
Aquí, { } representa el conjunto vacío Ø, y {A,B,C} el conjunto completo, es decir, los subconjuntos impropios de X.
Según la definición, tanto el conjunto vacío como el conjunto completo X son conjuntos abiertos.
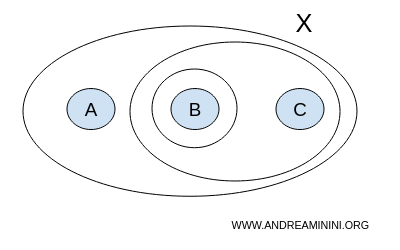
Una topología se compone de conjuntos abiertos, y, por definición, tanto la unión como la intersección de conjuntos abiertos resultan en otro conjunto abierto.
En este caso, la unión de los subconjuntos considerados en T sigue formando parte de la colección T, cumpliendo así con la cerradura bajo la operación de unión.
$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$
$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$
Del mismo modo, la intersección de los subconjuntos en T también forma parte de la colección T, demostrando la cerradura bajo la operación de intersección.
$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$
$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$
Por tanto, la colección T es una topología del conjunto X ya que satisface todas las condiciones requeridas.
Ejemplo 2
Veamos ahora una colección un poco diferente al ejemplo previo.
El conjunto X se mantiene sin cambios.
$$ X = \{ A,B,C \} $$
En este escenario, sin embargo, la colección T incluye además el subconjunto {A}, junto a los subconjuntos { }, {A,B,C}, {B}, {B,C}.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Esta nueva colección T no constituye una topología del conjunto X, ya que no cumple con todas las condiciones necesarias.
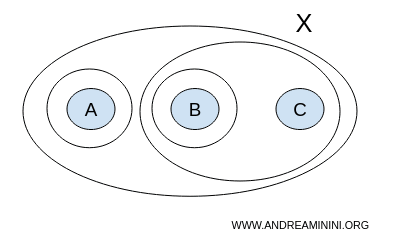
Por ejemplo, la unión de los subconjuntos {A} y {B} da como resultado el conjunto {A,B}, el cual no forma parte de la colección T.
$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\notin} T $$
Esto significa que, aunque los conjuntos {A} y {B} se consideran "abiertos" al estar en la colección T, su unión no genera otro conjunto abierto {A,B} al no encontrarse dentro de la colección.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Violando así una de las condiciones esenciales para que una colección sea considerada una topología de conjuntos abiertos.
Por lo tanto, la colección T no puede ser considerada una topología del conjunto X.
Y así sucesivamente