Grafo Topológico
Un grafo topológico es un espacio topológico que se obtiene a partir de un conjunto finito de puntos, llamados "vértices", y un conjunto finito de intervalos cerrados, disjuntos entre sí, en \(\mathbb{R}\), conocidos como "aristas". Estas aristas se conectan a los vértices siguiendo reglas específicas.
La topología de este espacio viene determinada por la forma en que se realizan estas conexiones, proporcionando al grafo topológico una representación dual: tanto geométrica como topológica, que refleja la red de relaciones entre los vértices.
Este procedimiento da lugar a un nuevo espacio que modeliza la estructura de un grafo.
Nota. Se trata de un caso particular de topología cociente, ya que consiste en aplicar una topología sobre un espacio para generar otro nuevo, denominado "espacio inducido". El nuevo espacio se construye uniendo un conjunto de intervalos a un conjunto de vértices. Dicho de otro modo, partimos de espacios sencillos (como intervalos cerrados) y los transformamos al adherirlos a determinados puntos, obteniendo así un espacio topológico más elaborado.
Cómo Construir un Grafo Topológico
La construcción de un grafo topológico puede descomponerse en dos etapas principales:
- Vértices: Se parte de un conjunto finito de puntos, denominados vértices. Por ejemplo, podemos etiquetarlos como A, B, C, D, E y F.
- Aristas: A continuación, se consideran un conjunto de intervalos (líneas) cada uno con dos extremos. Estos extremos se "adhieren" (o conectan) a vértices específicos, estableciendo enlaces. Estos enlaces, o intervalos, reciben el nombre de aristas.
En esencia, el procedimiento consiste en conectar intervalos a vértices para formar una estructura que denominamos grafo.
Se habla de grafo "topológico" porque su construcción depende de cómo se ensamblan o conectan entre sí los distintos espacios.
Un Ejemplo Práctico
Consideremos tres intervalos cerrados distintos en \(\mathbb{R}\):
$$ I_1 = [0, 1], \quad I_2 = [0, 1], \quad I_3 = [0, 1] $$
Se trata de segmentos de recta sencillos, cuyos extremos son \(0\) y \(1\).
Ahora definimos un conjunto $ G $ formado por 3 vértices, que llamaremos \(A\), \(B\) y \(C\):
$$ G = \{ A, B, C \} $$
Estos vértices son simplemente puntos a los cuales se unirán los extremos de los intervalos.
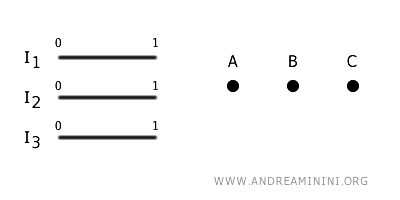
Procedemos entonces a aplicar la operación de topología cociente, conectando los extremos de los intervalos a vértices concretos:
- Se une el extremo \(0\) del intervalo \(I_1\) al vértice \(A\) y el extremo \(1\) del \(I_1\) al vértice \(B\).
- Se une el extremo \(0\) del intervalo \(I_2\) al vértice \(B\) y el extremo \(1\) del \(I_2\) al vértice \(C\).
- Se une el extremo \(0\) del intervalo \(I_3\) al vértice \(A\) y el extremo \(1\) del \(I_3\) al vértice \(C\).
El resultado es un grafo con tres vértices \(A\), \(B\) y \(C\) y tres aristas: $ (A, B) $, $ (B, C) $ y $ (A, C) $.
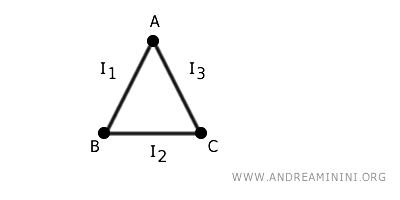
De este modo, a partir de intervalos separados y uniendo sus extremos a vértices, hemos construido una nueva estructura: el grafo topológico.
En definitiva, construir el grafo consiste en "ensamblar" los intervalos en torno a los vértices.
Y este proceso puede continuarse y extenderse a construcciones más complejas.