Continuidad en Topología

Sean $X$ y $Y$ dos espacios topológicos. Una función $f: X \to Y$ se dice continua si, para todo conjunto abierto $V$ en $Y$, la preimagen $f^{-1}(V)$ es un conjunto abierto en $X$.

En otras palabras, una función continua en topología "preserva" la estructura de los conjuntos abiertos al trasladar puntos de un espacio a otro.

La continuidad en topología se centra en mantener la "coherencia" de los conjuntos abiertos entre distintos espacios.

Nota: La continuidad en topología es un concepto más general que la continuidad en el análisis matemático, donde se basa en la noción de distancia entre puntos. En análisis, la continuidad se refiere a la cercanía entre puntos; en topología, se enfoca en cómo una función interactúa con la estructura de los conjuntos abiertos. En esencia, la definición topológica nos permite determinar si una función "respeta" la estructura de los conjuntos abiertos, incluso en contextos donde la distancia no es relevante.

Por ejemplo, "estirar" o "deformar" una figura geométrica sin rasgarla puede describirse mediante una función continua.

La continuidad garantiza que la estructura original (en particular, los conjuntos abiertos) permanezca intacta tras la transformación.

Un Ejemplo Práctico
El teorema de la base para la continuidad
Continuidad en topologías más gruesas y más finas
Diferencia entre conexidad y continuidad
Notas

Un Ejemplo Práctico

Consideremos dos espacios topológicos $X = \{a, b, c, d\}$ y $Y = \{1, 2\}$.

En $X$, los conjuntos abiertos son: $\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}$.
En $Y$, los conjuntos abiertos son: $\{\}, \{1\}, \{1, 2\}$.

Definimos una función $f: X \rightarrow Y$ de la siguiente manera:

$ f(a) = 1 $, $ f(b) = 1 $, $ f(c) = 2 $, $ f(d) = 2 $

¿Es continua esta función según la definición topológica?

Para ilustrarlo, representamos la función $f$ y ambos espacios topológicos, resaltando los conjuntos abiertos en cada uno.

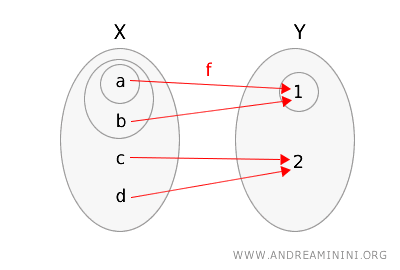
un ejemplo de continuidad topológica

Comprobemos ahora si se satisface la definición de continuidad:

Consideremos el conjunto abierto $\{1\}$ en $Y$; su preimagen en $X$ es $ f^{-1}(\{1\}) = \{a, b\} $. Este conjunto es abierto en $X$.
Consideremos el conjunto abierto $\{1, 2\}$ en $Y$; su preimagen es $ f^{-1}(\{1, 2\}) = \{a, b, c, d\} $. También es abierto en $X$.

No es necesario verificar el conjunto vacío, ya que siempre es abierto en cualquier topología.

En conclusión, dado que la preimagen de todo conjunto abierto en $Y$ es un conjunto abierto en $X$, la función $ f $ es continua.

Ejemplo 2

Veamos ahora otra función $g: X \rightarrow Y$ entre los mismos espacios:

$ g(a) = 1 $, $ g(b) = 1 $, $ g(c) = 1 $, $ g(d) = 2 $

Representamos la función $g$ y los dos espacios topológicos, destacando los conjuntos abiertos relevantes.

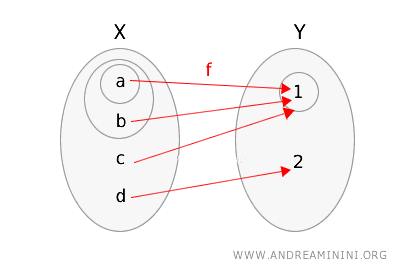
ejemplo de función no continua

Verifiquemos ahora la continuidad:

El conjunto abierto $\{1\}$ en $Y$ tiene como preimagen en $X$ el conjunto $ g^{-1}(\{1\}) = \{a, b, c\} $, que no es abierto en $X$.

Como existe al menos un conjunto abierto en $Y$ cuya preimagen no es abierta en $X$, concluimos que la función $g$ no es continua.

Ejemplo 3

Consideremos ahora la función identidad $ id: X \to X $ definida por $ id(x) = x $ para todo $ x \in X $.

$$ x = f(x) $$

En esencia, la función identidad no altera los elementos del espacio. Desde un punto de vista topológico, esto significa que la imagen de un conjunto abierto en $X$ sigue siendo abierta en $X$.

Por tanto, la función identidad $ f(x) = x $ es siempre continua, ya que no modifica la estructura topológica del espacio.

Ejemplo 4

Ahora consideremos una función constante $ f: X \to Y $ definida como $ f(x) = c $ para todo $ x \in X $.

$$ f(x) = c $$

Esto quiere decir que, sin importar qué elemento de $X$ elijamos, la función constante siempre devuelve el mismo valor $c$.

Según la definición topológica, para que $f$ sea continua, la preimagen de todo conjunto abierto en $Y$ debe ser un conjunto abierto en $X$.

Se pueden presentar dos situaciones:

Si $c$ pertenece a $V$, entonces $ f^{-1}(V) = X $, que es abierto.
Si $c$ no pertenece a $V$, entonces $ f^{-1}(V) = \emptyset $, que también es abierto.

En ambos casos, la preimagen es un conjunto abierto en $X$.

Así pues, la función constante $ f(x) = c $ es continua.

Nota: Este ejemplo muestra que la continuidad de una función topológica depende tanto de su definición como de la estructura de los espacios implicados. Para la función constante, la preimagen de cualquier conjunto abierto en $Y$ siempre resulta ser abierta en $X$, asegurando su continuidad.

Ejemplo 5

Finalmente, consideremos nuevamente la función identidad $ f : X \to Y $, definida por $ f(x) = x $, pero esta vez entre dos espacios diferentes:

$X$ es el conjunto de los números reales $ \mathbb{R} $ con la topología estándar, donde los abiertos son intervalos del tipo $ (a, b) $.
$Y$ es el conjunto de los números reales $ \mathbb{R} $ con la topología del límite inferior, donde los abiertos son intervalos del tipo $[a, b)$.

Para saber si $f$ es continua, debemos verificar si la preimagen de un conjunto abierto en $Y$ es abierta en $X$.

Consideremos el conjunto abierto $ [0, 1) $ en $Y$, que es abierto en la topología del límite inferior.

La preimagen de $ [0, 1) $ mediante $f$ es $ [0, 1) $, ya que $f$ es la identidad.

No obstante, $ [0, 1) $ no es abierto en la topología estándar.

Nota: En la topología estándar, un conjunto es abierto si, alrededor de cada punto, existe un intervalo contenido completamente en el conjunto. En $ [0, 1) $, el punto $0$ no cumple esta condición, ya que cualquier entorno incluiría números negativos.

Por tanto, la función identidad $ f : \mathbb{R} \to \mathbb{R} $, con $ \mathbb{R} $ dotado de distintas topologías en dominio y codominio, no es continua.

Este ejemplo pone de manifiesto que la continuidad en topología depende no sólo de la función, sino también de las topologías de los espacios considerados.

Aunque la función identidad $f(x) = x$ es la misma, en este caso no resulta continua.

El teorema de la base para la continuidad

Sean $X$ y $Y$ dos espacios topológicos. Una función $f: X \to Y$ es continua si, y solo si, para todo conjunto base $B_Y$ de la topología de $Y$, la preimagen $f^{-1}(B_Y)$ es un conjunto abierto en $X$.

Este teorema resulta especialmente útil porque simplifica considerablemente el proceso de verificación de la continuidad de una función.

En lugar de comprobar la preimagen de cada conjunto abierto de $Y$, basta con verificar la preimagen de una colección mucho más reducida: los conjuntos que forman una base de la topología de $Y$.

Esto disminuye de manera significativa el número de comprobaciones necesarias, facilitando y agilizando la verificación de la continuidad.

Demostración. Todo conjunto abierto de $Y$ puede expresarse como unión de conjuntos de su base $B_Y$. Por tanto, si la preimagen de cada conjunto de la base es abierta en $X$, la preimagen de cualquier conjunto abierto (como unión de preimágenes de conjuntos base) también será abierta en $X$. De este modo, se cumple la condición de continuidad y, por tanto, la función $f: X \to Y$ es continua.

Ejemplo

Consideremos dos espacios topológicos $X = \{a, b, c, d\}$ y $Y = \{x, y, z\}$, con las siguientes topologías:

La topología de $X$ es $ \tau_X = \{\emptyset, \{a\}, \{a, b\}, \{a, b, c, d\}\} $.
La topología de $Y$ tiene como base $B_Y = \{\{x\}, \{y\}, \{z\}\}$.

En este caso, la topología completa de $Y$ se genera mediante uniones de elementos de su base, lo que permite construir muchos conjuntos abiertos que no son elementos individuales de la base, sino uniones de ellos.

Por ejemplo, los conjuntos $ \{x, y\} $, $ \{x, z\} $, $ \{y, z\} $ y $ \{x, y, z\} $ no forman parte de la base $B_Y$, pero siguen siendo abiertos en $Y$ al ser uniones de conjuntos de la base.

Definimos ahora una función $f: X \to Y$ de la siguiente manera:

$f(a) = x$
$f(b) = x$
$f(c) = y$
$f(d) = z$

Para determinar si la función es continua, debemos comprobar si las preimágenes de los conjuntos de la base $B_Y = \{\{x\}, \{y\}, \{z\}\}$ son abiertas en $X$.

$f^{-1}(\{x\}) = \{a, b\}$, que es un conjunto abierto en $X$.
$f^{-1}(\{y\}) = \{c\}$, que no es abierto en $X$, ya que $ \{c\} $ no pertenece a la topología $ \tau_X $.

Como la preimagen de $ \{y\} $ no es un conjunto abierto en $X$, concluimos que la función $f$ no es continua.

Nota. Si la preimagen de un conjunto de la base no es abierta, no es necesario seguir comprobando otras preimágenes. Basta encontrar un solo conjunto cuya preimagen no sea abierta para concluir que la función no es continua.

Continuidad en topologías más gruesas y más finas

Si una función es continua respecto de una topología más gruesa, entonces también será continua respecto de cualquier topología más fina sobre el mismo conjunto.

No obstante, la recíproca no siempre es cierta: una función puede ser continua en la topología más fina, pero no en la más gruesa.

Diferencia entre topologías más fina y más gruesa. Dadas dos topologías sobre el mismo conjunto $X$, una se dice más gruesa si tiene menos conjuntos abiertos, y más fina si posee más conjuntos abiertos.

Ejemplo

Consideremos el conjunto $X = \{a, b\}$ con dos topologías:

Topología más gruesa $ \tau_1 = \{\varnothing, \{a, b\}\} $, donde solo el conjunto vacío y el conjunto total son abiertos.
Topología más fina $ \tau_2 = \{\varnothing, \{a\}, \{b\}, \{a, b\}\} $, donde también son abiertos los conjuntos $\{a\}$ y $\{b\}$.

Definimos una función $f: X \to Y$, donde $Y = \{1\}$, como:

$$ f(a) = 1 $$

$$ f(b) = 1 $$

En la topología más gruesa $ \tau_1 $, los conjuntos abiertos son $ \varnothing $ y $ \{a, b\} $.

Comprobemos la continuidad de $f$:

$ f^{-1}(\varnothing) = \varnothing $, que es abierto en $ \tau_1 $.
$ f^{-1}(\{1\}) = \{a, b\} $, que también es abierto en $ \tau_1 $.

Por tanto, la función $f$ es continua respecto de la topología más gruesa $ \tau_1 $.

Como los conjuntos abiertos de $ \tau_1 $ también son abiertos en $ \tau_2 $, la función $f$ es continua respecto de la topología más fina $ \tau_2 $ igualmente.

En $ \tau_2 $, los conjuntos abiertos son $ \varnothing $, $ \{a\} $, $ \{b\} $ y $ \{a, b\} $.

$ f^{-1}(\varnothing) = \varnothing $, abierto en $ \tau_2 $.
$ f^{-1}(\{1\}) = \{a, b\} $, abierto en $ \tau_2 $.

En consecuencia, $f$ es continua en ambas topologías.

Sin embargo, la recíproca no es válida en general. Puede ocurrir que una función sea continua respecto de una topología más fina pero no respecto de una más gruesa, debido a la menor cantidad de abiertos en la topología más gruesa.

Ejemplo 2

Analicemos nuevamente el conjunto $ X = \{a, b\} $ dotado de las mismas topologías:

Topología más gruesa: $ \tau_1 = \{\varnothing, \{a, b\}\} $
Topología más fina: $ \tau_2 = \{\varnothing, \{a\}, \{b\}, \{a, b\}\} $

Definimos ahora una función $ g: X \to Y $, donde $ Y = \{1, 2\} $, de la siguiente forma:

$$ g(a) = 1 $$

$$ g(b) = 2 $$

La función $g$ es continua respecto de la topología más fina $ \tau_2 $ porque todas las preimágenes de los conjuntos de $Y$ son abiertas en $ \tau_2 $:

$ g^{-1}(\varnothing) = \varnothing $, abierto en $ \tau_2 $.
$ g^{-1}(\{1,2\}) = \{a,b\} $, abierto en $ \tau_2 $.
$ g^{-1}(\{1\}) = \{a\} $, abierto en $ \tau_2 $.
$ g^{-1}(\{2\}) = \{b\} $, abierto en $ \tau_2 $.

No obstante, la función $g$ no es continua respecto de la topología más gruesa $ \tau_1 $, ya que algunas de las preimágenes no son conjuntos abiertos en $ \tau_1 $:

$ g^{-1}(\varnothing) = \varnothing $, abierto en $ \tau_1 $.
$ g^{-1}(\{1,2\}) = \{a,b\} $, abierto en $ \tau_1 $.
$ g^{-1}(\{1\}) = \{a\} $, que no es abierto en $ \tau_1 $.

Por tanto, la función $g$ es continua respecto de la topología más fina $ \tau_2 $, pero no respecto de la topología más gruesa $ \tau_1 $.

Diferencia entre conexidad y continuidad

En topología, la conexidad y la continuidad son conceptos diferentes, aunque ambos describen cómo se relacionan los puntos dentro de un espacio topológico. Comprender esta distinción es fundamental para entender la estructura y el comportamiento de los espacios topológicos.

La conexidad: una propiedad del espacio
Un espacio topológico $ X $ se dice conexo si no puede descomponerse en la unión de dos subconjuntos disjuntos que sean ambos abiertos (o, de forma equivalente, ambos cerrados). En términos intuitivos, un espacio conexo es aquel que no puede “dividirse” en partes separadas sin perder su unidad topológica. La conexidad es, por tanto, una propiedad intrínseca del espacio, independiente de cualquier aplicación definida sobre él.
La continuidad: una propiedad de las aplicaciones
La continuidad se refiere a una aplicación $ f: X \to Y $ entre dos espacios topológicos. Se dice que $ f $ es continua si la preimagen de todo conjunto abierto de $ Y $ es un conjunto abierto en $ X $. En otras palabras, una función continua preserva la estructura topológica del dominio, evitando “saltos” o “roturas” en la correspondencia entre los puntos. Por ejemplo, la función $ f(x) = x^2 $ es continua de $ \mathbb{R} $ en $ \mathbb{R} $ con la topología usual, pero este hecho no implica nada sobre la conexidad del propio $ \mathbb{R} $.

Aunque existen teoremas que relacionan la conexidad y la continuidad, ambos conceptos conservan naturalezas distintas.

Por ejemplo, si $ X $ es conexo y $ f: X \to Y $ es continua, entonces la imagen $ f(X) $ es un subconjunto conexo de $ Y $.

En síntesis, la continuidad preserva la conexidad, pero mientras la conexidad caracteriza la estructura global del espacio, la continuidad describe el comportamiento de las aplicaciones que actúan sobre él.

Notas

Algunas consideraciones adicionales sobre la continuidad en topología:

Una función continua no es necesariamente una función abierta
Una función continua no siempre lleva conjuntos abiertos en conjuntos abiertos. Así, la continuidad no implica preservar abiertos, a diferencia de lo que ocurre con las funciones abiertas.
Lema del pegado
Sean $ f: A \to Y $ y $ g: B \to Y $ funciones continuas definidas en conjuntos $ A $ y $ B $ que coinciden en su intersección. En tal caso, se pueden "pegar" para construir una función continua $ h $ definida en $ A \cup B $.
Continuidad en la topología subespacio
Si $ Y $ es un subconjunto de un espacio topológico $ X $, la función inclusión $ f: Y \to X $, definida por $ f(y) = y $ para todo $ y \in Y $, es continua.
Continuidad en la topología cociente
Dada una aplicación suprayectiva $ f: X \to A $ desde un espacio topológico $X$, se define la topología cociente en $A$ de manera que $f$ sea continua.
Teorema sobre la continuidad del cierre
La continuidad de $ f $ garantiza que, si un punto $ x \in X $ pertenece al cierre de un conjunto $ A \subset X $, entonces $ f(x) $ pertenece al cierre de $ f(A) $.
Definición de continuidad mediante conjuntos abiertos
Una función es continua si, y solo si, la preimagen de cada conjunto abierto $ U \subset Y $ es abierta en $ X $.
Definición de continuidad mediante conjuntos cerrados
La función $ f: X \to Y $ es continua si, y solo si, la preimagen de todo conjunto cerrado $ C \subset Y $ es un conjunto cerrado en $ X $.
Teorema sobre la composición de funciones continuas
La composición $ g \circ f $ de dos funciones continuas $ f $ y $ g $ también es continua.
Continuidad y sucesiones convergentes
Si $ f: X \to Y $ es continua y una sucesión $ x_1, x_2, \dots $ en $X$ converge a $x$, entonces la sucesión $ f(x_1), f(x_2), \dots $ converge a $ f(x) $ en $Y$.
Funciones polinómicas
En el espacio topológico $ \mathbb{R} $ con la topología estándar, toda función polinómica $ p : \mathbb{R} \to \mathbb{R} $, donde $ p(x) = a_nx^n + \dots + a_1x + a_0 $, es continua.

Y así sucesivamente.