Definición de continuidad mediante conjuntos abiertos

Una función $ f : X \to Y $ es continua si, y solo si, para todo punto $ x \in X $ y todo conjunto abierto $ U \subset Y $ que contiene a $ f(x) $, existe un entorno $ V $ de $ x $ tal que $ f(V) \subset U $.

En otras palabras, una función $ f: X \to Y $ es continua si la preimagen $ f^{-1}(U) $ es un conjunto abierto en $ X $ para todo conjunto abierto $ U \subset Y $.

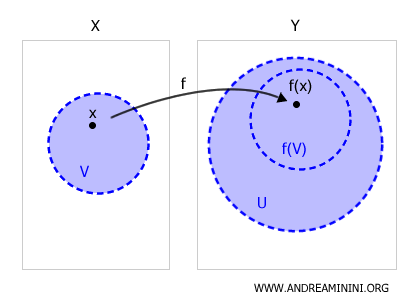
ilustración de la continuidad

La continuidad implica que la preimagen de cualquier conjunto abierto del codominio es siempre un conjunto abierto en el dominio.

Este teorema proporciona una definición topológica de continuidad basada en la estructura de los conjuntos abiertos en ambos espacios.

Se la conoce también como la definición de continuidad mediante conjuntos abiertos.

Nota: Este resultado también se denomina “equivalencia de definiciones de continuidad”, ya que muestra que las dos formulaciones clásicas de continuidad - la topológica mediante conjuntos abiertos y la analítica mediante $\varepsilon$-$\delta$ - son equivalentes. La definición analítica establece que: "Una función $ f $ es continua en un punto $ x_0 \in \mathbb{R} $ si, para todo $\varepsilon > 0$, existe un $\delta > 0$ tal que, para todo $ x \in \mathbb{R} $, si $ |x - x_0| < \delta $, entonces $ |f(x) - f(x_0)| < \varepsilon $", una noción que suele introducirse en los cursos básicos de cálculo.

También se puede caracterizar la continuidad en términos de conjuntos cerrados: una función es continua si la preimagen de todo conjunto cerrado es también un conjunto cerrado.

En efecto, dada una función $ f: X \to Y $ entre espacios topológicos, $ f $ es continua si y solo si la preimagen $ f^{-1}(C) $ de todo conjunto cerrado $ C \subset Y $ es un conjunto cerrado en $ X $.

Esto refleja cómo la continuidad puede describirse tanto con conjuntos abiertos como con cerrados, dado que en topología estos conceptos son complementarios y estrechamente vinculados.

Un ejemplo práctico
Demostración

Un ejemplo práctico

Consideremos la función $ f : \mathbb{R} \to \mathbb{R} $ dada por $ f(x) = x^2 $.

Queremos verificar su continuidad utilizando la definición topológica basada en conjuntos abiertos.

Según esta definición, $ f $ es continua si para todo conjunto abierto $ U \subset \mathbb{R} $ y todo $ x \in f^{-1}(U) $, existe un entorno $ V $ de $ x $ tal que $ f(V) \subset U $.

Tomemos, por ejemplo, el conjunto abierto $ U = (1, 4) $, que contiene todos los números reales entre 1 y 4.

intervalo abierto de ejemplo

Analicemos ahora $ f^{-1}(U) $, es decir, los valores de $ x \in \mathbb{R} $ tales que $ x^2 \in (1, 4) $.

Buscamos los valores de $ x $ que satisfacen:

$$ 1 < x^2 < 4 $$

Lo cual implica:

$$ 1 < |x| < 2 $$

Es decir, $ x $ pertenece al conjunto $ (-2, -1) \cup (1, 2) $, que es claramente abierto en $ \mathbb{R} $.

Hemos identificado $ f^{-1}(U) $, y vemos que se trata de un conjunto abierto.

Ahora, tomemos un punto cualquiera $ x \in f^{-1}(U) $; por ejemplo, $ x = 1.5 $.

Evaluamos $ f(1.5) = 2.25 $, valor que pertenece a $ U = (1, 4) $.

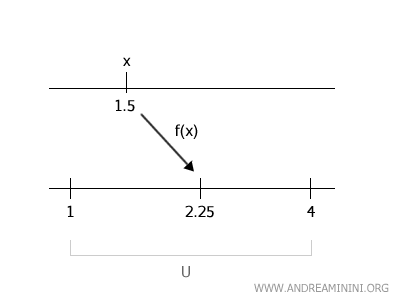
verificación puntual de la continuidad

Busquemos un entorno $ V $ de $ x = 1.5 $ tal que $ f(V) \subset (1, 4) $.

Por ejemplo, podemos tomar el intervalo $ V = (1.4, 1.6) $.

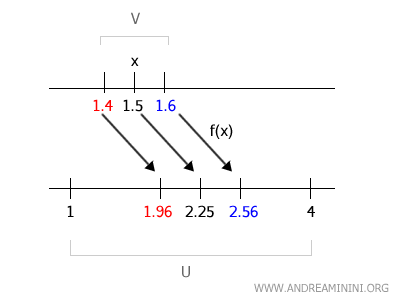
entorno alrededor del punto

Calculamos los extremos de la imagen de este entorno:

$$ f(1.4) = 1.96 \quad \text{y} \quad f(1.6) = 2.56 $$

Por tanto, $ f(V) = (1.96, 2.56) \subset (1, 4) = U $.

Esto verifica que para cualquier $ x \in f^{-1}(U) $, existe un entorno $ V $ de $ x $ tal que $ f(V) \subset U $, cumpliéndose la condición de continuidad.

Como esta propiedad se cumple para todo $ x \in \mathbb{R} $, concluimos que la función $ f(x) = x^2 $ es continua en todo su dominio.

Nota: Para que una función sea continua, la propiedad debe cumplirse en todos los puntos $ x \in X $, no basta con verificarla en uno solo. La continuidad es una propiedad global que debe mantenerse a lo largo de todo el dominio. En el caso de $ f : \mathbb{R} \to \mathbb{R} $, hay que demostrar que para todo $ x \in \mathbb{R} $ y todo conjunto abierto $ U $ que contenga a $ f(x) $, existe un entorno $ V $ de $ x $ tal que $ f(V) \subset U $.

Demostración

Dividiremos la demostración en dos partes:

A] Primera parte

Supongamos que la función $ f $ es continua en el sentido topológico.

Tomamos un punto $ x \in X $ y un conjunto abierto $ U \subset Y $ tal que $ f(x) \in U $.

Definimos $ V = f^{-1}(U) $, es decir, el conjunto de puntos en $ X $ cuya imagen mediante $ f $ pertenece a $ U $.

Como $ f $ es continua, $ V $ es abierto en $ X $.

Entonces, dado que $ x \in V $ y $ f(V) \subset U $, se cumple la condición deseada: para todo conjunto abierto que contiene a $ f(x) $, existe un entorno abierto de $ x $ que se mapea dentro de él.

B] Segunda parte

Supongamos ahora que, para todo $ x \in X $ y para todo conjunto abierto $ U \subset Y $ que contiene a $ f(x) $, existe un entorno $ V $ de $ x $ tal que $ f(V) \subset U $.

Queremos demostrar que $ f^{-1}(W) $ es abierto en $ X $ para todo conjunto abierto $ W \subset Y $.

Tomamos un punto $ x \in f^{-1}(W) $, es decir, tal que $ f(x) \in W $.

Por hipótesis, existe un entorno $ V_x $ de $ x $ tal que $ f(V_x) \subset W $.

Esto implica que $ V_x \subset f^{-1}(W) $, y por tanto $ f^{-1}(W) $ contiene un entorno abierto alrededor de cada uno de sus puntos.

Como esto es válido para todo $ x \in f^{-1}(W) $, concluimos que $ f^{-1}(W) $ es abierto en $ X $.

Conclusión

En definitiva, las definiciones de continuidad basadas en conjuntos abiertos y en entornos son completamente equivalentes.

Y así sucesivamente.