Espacios simplemente conexos en topología
Se dice que un espacio topológico es simplemente conexo si cualquier camino cerrado dentro de él puede transformarse continuamente hasta reducirse a un punto.
En palabras más simples, un espacio es simplemente conexo si es posible contraer cualquier lazo a un punto sin necesidad de salir del espacio.
Esto sugiere que el espacio es un bloque coherente (espacio conectado) y no presenta "huecos" internos.
Nota: De esto se deduce que un espacio simplemente conexo también es un espacio conectado. No obstante, el inverso no es necesariamente cierto: no todos los espacios conectados son simplemente conexos.
Un Ejemplo Práctico
Consideremos, por ejemplo, una esfera, que es un espacio topológico simplemente conexo porque cualquier curva cerrada en su interior puede colapsarse a un solo punto.
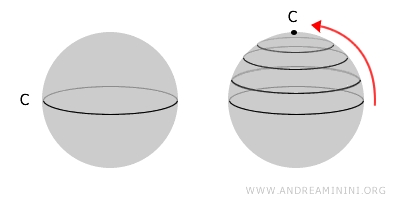
Por otro lado, un toro, o "rosquilla", no es simplemente conexo debido a su agujero central, que impide que ciertos lazos se reduzcan a un punto.
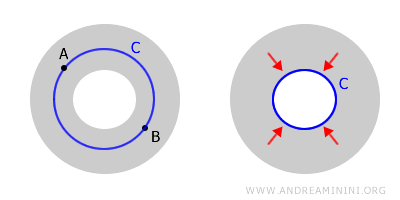
Este ejemplo también ilustra que estar conectado no garantiza la simple conectividad.
La "rosquilla" es un espacio conectado porque es posible unir cualquier par de puntos A y B mediante un camino que permanezca dentro del espacio.
No obstante, la "rosquilla" no es simplemente conexa porque no todas sus curvas cerradas pueden ser contraídas a un punto.
En estos ejemplos, donde un espacio está conectado pero no simplemente conexo, se considera un espacio múltiplemente conectado. Algunos ejemplos son la región anular o el espacio toroidal.
Así, la simple conectividad es una condición más estricta que la conectividad por arcos.
Y así sucesivamente.