Conexidad en topología

En topología, un espacio se dice conexo si no puede expresarse como la unión de dos conjuntos abiertos, disjuntos y no vacíos. Dicho de otro modo, un espacio es conexo cuando no admite una separación en abiertos.

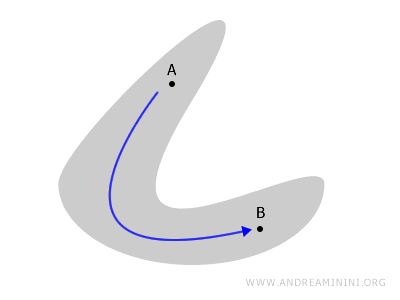
La conexidad describe cómo las distintas partes de un espacio topológico permanecen unidas, sin quedar fragmentadas en regiones independientes.

Se trata de una propiedad puramente topológica, ya que se define exclusivamente en términos de conjuntos abiertos y no depende de distancias, ángulos ni medidas.

Junto con la continuidad, la conexidad es uno de los conceptos fundamentales de la topología general.

La conexidad desempeña un papel central en muchas áreas de las matemáticas, ya que permite comprender la estructura global de los espacios topológicos y analizar cómo se organizan sus componentes.

Un ejemplo intuitivo

Consideremos un espacio geométrico, como una figura plana o un sólido. Diremos que es conexo si no es posible dividirlo en dos regiones abiertas, separadas y no vacías.

Intuitivamente, el espacio “forma una sola pieza”.

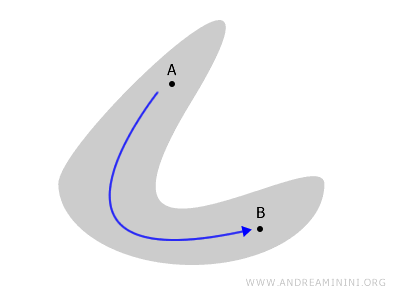
En cambio, si el espacio puede descomponerse en dos partes separadas, entonces no es conexo. En ese caso se dice que el espacio es disconexo.

Por ejemplo, en la situación siguiente el espacio está dividido en dos subconjuntos disjuntos. No existe forma de pasar de un punto A a un punto B sin abandonar el espacio.

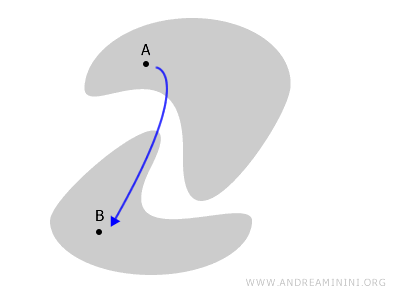
Para comprender mejor esta idea, resulta útil analizar un ejemplo cotidiano.

¿Cuándo un espacio es disconexo?

Imaginemos dos habitaciones separadas dentro de un edificio, divididas por una pared. Cada habitación representa un conjunto abierto, y la pared no forma parte de ninguno de ellos.

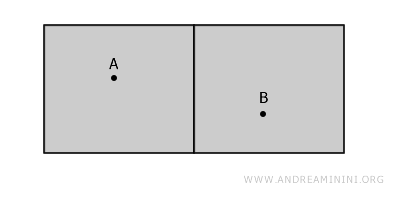
Aunque las habitaciones estén próximas, el espacio no es conexo, ya que cualquier recorrido desde un punto A hasta un punto B exige atravesar la pared, que no pertenece al espacio considerado.

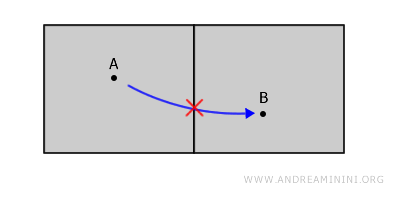
Este ejemplo pone de manifiesto un aspecto clave: los bordes o paredes no pertenecen a los conjuntos abiertos y, por tanto, no pueden utilizarse para “conectar” las regiones.

Conexidad local

Un espacio topológico es localmente conexo si todo punto posee un entorno abierto que es conexo. Es decir, alrededor de cada punto existe una región pequeña que no se descompone en partes separadas.

Consideremos de nuevo el ejemplo de las dos habitaciones separadas.

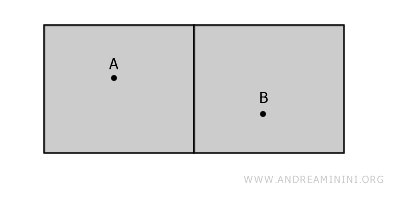
El espacio completo es disconexo, ya que no existe forma de unir los puntos A y B sin salir del espacio.

Sin embargo, alrededor del punto A existe un entorno contenido en una sola habitación, dentro del cual todos los puntos permanecen unidos. Esto muestra que el espacio es localmente conexo en A.

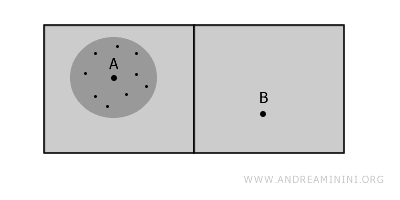
De manera análoga, el punto B también posee entornos abiertos conexos.

Tipos de conexidad

En topología se distinguen varias nociones de conexidad. Las más importantes son las siguientes:

• Conexidad
  Un espacio topológico \( X \) es conexo si no puede escribirse como la unión de dos conjuntos abiertos, disjuntos y no vacíos. En otras palabras, el espacio no admite una separación.

  Ejemplo. El intervalo \( (-1,1) \) es conexo, mientras que el conjunto \( (-1,0) \cup (0,1) \) no lo es, ya que puede descomponerse en dos abiertos disjuntos y no vacíos cuya unión es todo el espacio. Estos dos conjuntos constituyen una separación.

• Conexidad por trayectorias
  Un espacio topológico es conexo por trayectorias si, para cualquier par de puntos A y B, existe un camino continuo que los une y permanece completamente dentro del espacio. Todo espacio conexo por trayectorias es conexo, pero no todo espacio conexo es conexo por trayectorias.

  Por ejemplo, en una región cerrada del plano, es posible unir dos puntos interiores mediante una curva continua sin salir de la figura.
  
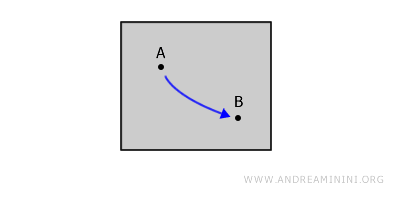
  Diferencia entre trayectorias y arcos. En la conexidad por arcos, el camino debe ser inyectivo, es decir, no puede cortarse ni pasar dos veces por el mismo punto.

• Espacios simplemente conexos
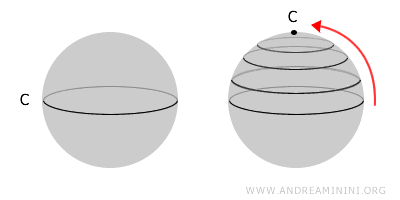
  Un espacio es simplemente conexo si es conexo y, además, todo lazo cerrado puede deformarse continuamente hasta reducirse a un punto. En términos formales, todo lazo es homotópico a una aplicación constante.

  Una esfera es simplemente conexa, ya que cualquier lazo puede contraerse a un punto. En cambio, un toro no lo es, debido a la presencia de un “agujero” central.
  
  
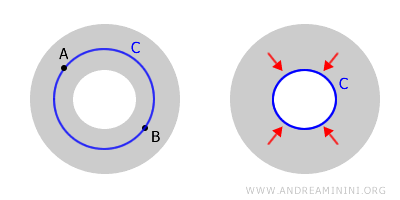
  Estos espacios, conexos pero no simplemente conexos, suelen describirse como espacios con múltiples clases de lazos no contráctiles.

Observaciones

• En la recta real \( \mathbb{R} \), los únicos subconjuntos conexos son los intervalos.