Separación de un subconjunto por abiertos

Sea $ A $ un subconjunto de un espacio topológico $ X $. Decimos que los abiertos $ U $ y $ V $ en $ X $ establecen una separación de $ A $ cuando se cumplen tres condiciones muy concretas:

Cubren todo el conjunto $ A $ \[ A \subseteq U \cup V \]
Cada uno de ellos contiene al menos un punto de $ A $ \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
No comparten ningún punto de $ A $ \[ U \cap V \cap A = \varnothing \]

Con estas condiciones, el conjunto $ A $ queda dividido en dos partes completamente separadas: una dentro de $ U $ y otra dentro de $ V $. No hay puntos de $ A $ que puedan estar en ambos abiertos a la vez, y esa es precisamente la idea de separación en topología.

Este enfoque es el modo habitual de describir, en términos topológicos, cuándo un subconjunto está realmente separado.

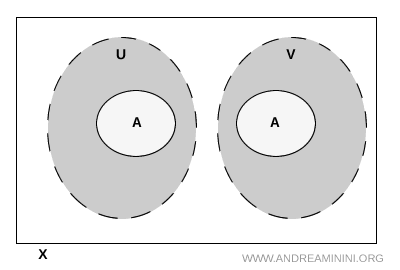
diagrama que representa la separación de un subconjunto mediante abiertos

Nota. Aunque $ U $ y $ V $ pueden llegar a intersectarse en otras zonas del espacio $ X $, esto no afecta a la separación. Lo importante es que su intersección no incluya ningún punto de $ A $.
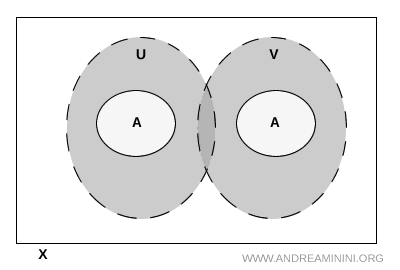
diagrama que muestra que los abiertos pueden intersectarse fuera de A

Un ejemplo práctico

Para ver la idea en acción, tomemos $ X = \mathbb{R} $ con su topología usual. Consideremos el conjunto:

$$ A = [-2,-1] \cup [1,2] $$

Está formado por dos intervalos cerrados que no se tocan.

Definimos ahora los siguientes abiertos de $ X $:

$$ U = (-3,0) $$

$$ V = (0,3) $$

Si los representamos en una recta numérica, obtenemos lo siguiente:

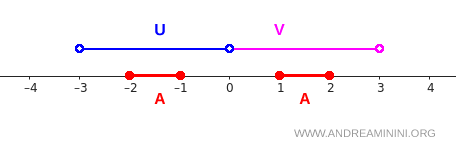
representación gráfica de U, V y el subconjunto A

El intervalo $ [-2,-1] $, que constituye una de las partes de $ A $, está completamente contenido en $ U $. Del mismo modo, el intervalo $ [1,2] $ está totalmente dentro de $ V $.

Así, la primera condición se cumple:

$$ A \subseteq U \cup V $$

Ambos abiertos contienen puntos de $ A $:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

Y no hay ningún punto de $ A $ que esté en $ U $ y en $ V $ al mismo tiempo:

$$ U \cap V \cap A = \varnothing $$

Con todo ello, queda claro que $ U $ y $ V $ forman una separación del conjunto $ A $ dentro del espacio $ X $.