Espacios conexos en topología
¿Qué significa que un espacio sea conexo?
Decimos que un espacio topológico $X$ es conexo cuando no puede dividirse en dos partes abiertas que estén completamente separadas entre sí. En otras palabras, no existen dos conjuntos abiertos no vacíos $U$ y $V$ tales que:
- $U \neq \emptyset$ y $V \neq \emptyset$ - ambos tengan puntos;
- $U \cap V = \emptyset$ - no compartan ningún punto;
- $U \cup V = X$ - juntos formen todo el espacio.
Si sí existe un par así, decimos que el espacio es disconexo.
De forma más intuitiva, un espacio es conexo cuando no puede “partirse” en dos regiones abiertas completamente separadas. Si se puede, el espacio está disconectado, y el par $(U, V)$ que lo divide se llama una separación.
Nota. Esta es la definición formal de conexidad topológica. Más adelante veremos que no siempre coincide con la idea de “conexión por caminos” o “conexión por arcos”.
Un ejemplo paso a paso
Imaginemos un conjunto $X$ formado por tres puntos:
$$ X = \{a, b, c\} $$
Sobre este conjunto podemos definir distintas topologías, es decir, diferentes formas de considerar qué subconjuntos son “abiertos”. Veamos dos ejemplos:
- Topología A
$$ \mathcal{T}_A = \{ \emptyset, X, \{a,b\}, \{b\}, \{b,c\} \} $$ - Topología B
$$ \mathcal{T}_B = \{ \emptyset, X, \{a,b\}, \{c\}, \{b,c\} \} $$
¿Cuál de los dos espacios resulta conexo?
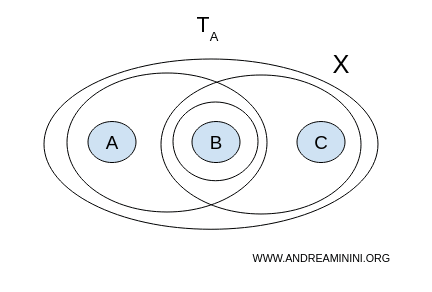
1) Topología A
Busquemos si hay dos conjuntos abiertos no vacíos, disjuntos y cuya unión cubra todo $X$.
- $U = \{a,b\}, V = \{b,c\}$ → no son disjuntos, comparten el punto $b$;
- $U = \{a,b\}, V = \{b\}$ → tampoco son disjuntos;
- $U = \{b\}, V = \{b,c\}$ → siguen sin serlo.
No hay forma de dividir el espacio sin que los conjuntos se superpongan. Por tanto, $X$ con la topología A es conexo.
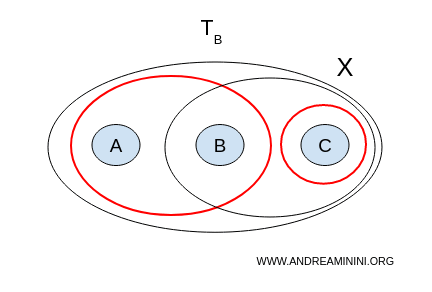
2) Topología B
Ahora hagamos lo mismo con $ \mathcal{T}_B = \{ \emptyset, X, \{a,b\}, \{c\}, \{b,c\} \} $.
- $U = \{a,b\}, V = \{b,c\}$ → no son disjuntos, comparten $b$;
- $U = \{a,b\}, V = \{c\}$ → son disjuntos, no vacíos y su unión da $X$.
En este caso sí aparece una separación válida. Por tanto, el espacio $X$ con la topología B es disconexo.
Nota. Este ejemplo muestra que la conexidad no depende solo del conjunto de puntos, sino de la topología que elijamos. Con los mismos elementos, una topología puede mantener el espacio unido, mientras otra lo separa.
Otro ejemplo: la recta real sin un punto
Consideremos ahora el espacio:
$$ X = (-\infty, n) \cup (n, +\infty) $$
que es la recta real sin el punto $n$:
$$ X = \mathbb{R} \setminus \{n\} $$
Tomemos los conjuntos $ U = (-\infty, n) $ y $ V = (n, +\infty) $.
- Ambos son abiertos en la topología usual de los reales.
- Son disjuntos (no comparten puntos).
- Y ambos son no vacíos.
Su unión cubre todo $X$, por lo tanto cumplen todas las condiciones de una separación.
$$ U \neq \emptyset, \quad V \neq \emptyset, \quad U \cap V = \emptyset, \quad U \cup V = X $$
El espacio $ X = (-\infty, n) \cup (n, +\infty) $ es disconexo, porque se puede dividir en dos partes abiertas completamente separadas.
Nota. Quitar un solo punto a la recta real “rompe” su continuidad: quedan dos regiones - una a la izquierda y otra a la derecha - que no pueden unirse mediante ningún camino continuo. Por eso este espacio no solo es disconexo, sino también no conexo por caminos.
Conexión topológica vs. conexión por caminos
Estas dos ideas están relacionadas, pero no son equivalentes.
Un espacio puede ser conexo sin serlo por caminos. Veamos la diferencia:
- Conexidad topológica
El espacio no puede dividirse en dos conjuntos abiertos, disjuntos y no vacíos, que juntos formen todo el espacio. - Conexidad por caminos
Cualquier par de puntos puede unirse mediante un camino continuo que permanezca dentro del espacio. Si ese camino no se cruza a sí mismo, el espacio se llama conexo por arcos.
En general, todo espacio conexo por caminos es conexo, pero no al revés: no todo espacio conexo es conexo por caminos.
La existencia de un camino continuo entre dos puntos impide que el espacio pueda “romperse” en regiones separadas. Sin embargo, algunos espacios, aunque sean conexos, no admiten caminos que unan ciertos puntos.
Ejemplo. El caso clásico es la curva del seno del topólogo:
$$ S = \{ (x, \sin(1/x)) \mid x > 0 \} \cup \{ (0, y) \mid -1 \le y \le 1 \} $$
Este espacio es conexo porque no puede dividirse en dos conjuntos abiertos disjuntos, pero no es conexo por caminos: no existe un camino continuo que una un punto de la curva oscilante con un punto del segmento vertical.
Así, la topología nos enseña que “estar conectado” no siempre significa “poder recorrerlo con un camino”.
Notas
Algunas ideas complementarias sobre los espacios conexos
- Teorema: caracterización de los espacios conexos mediante conjuntos abiertos y cerrados (clopen)
Un espacio topológico \( X \) se considera conexo cuando los únicos subconjuntos que son a la vez abiertos y cerrados (clopen) son el propio \( X \) y el conjunto vacío \( \emptyset \). Este criterio ofrece una forma sencilla y potente de reconocer si un espacio puede dividirse o no en partes independientes.
Existen otros teoremas y ejemplos que profundizan en esta idea y muestran cómo la conexión es una propiedad esencial en el estudio de la topología.