Todo conjunto conexo está contenido en una única componente conexa
Sean \( A \) y \( B \) subconjuntos de un espacio topológico \( X \), donde \( A \) es conexo y \( A \subset B \). Si el conjunto \( B \) admite una separación en dos subconjuntos \( B_1 \) y \( B_2 \) dentro de \( X \), entonces \( A \) debe quedar necesariamente contenido por completo en uno solo de ellos: $$ A \subset B_1 \quad \text{o} \quad A \subset B_2 $$
En otras palabras, un conjunto conexo no puede intersectar simultáneamente ambos lados de una separación.
Cuando un conjunto conexo está contenido en otro que se descompone en dos partes disjuntas, no puede “repartirse” entre ellas, sino que debe quedar íntegramente dentro de una sola.
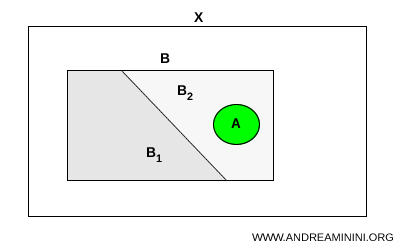
De forma intuitiva, puede pensarse un conjunto conexo como una cuerda continua colocada dentro de un sobre. Si el sobre se divide en dos compartimentos disjuntos mientras la cuerda permanece intacta, la cuerda solo puede quedar en uno de ellos. Para ocupar ambos, tendría que romperse. La conexidad expresa precisamente esta imposibilidad de “romper” el conjunto al atravesar una separación.
Un ejemplo concreto
Consideremos el espacio topológico:
$$ X = \mathbb{R} $$
y el siguiente subconjunto de \( X \):
$$ B = (-3,4) $$
Este conjunto puede separarse en los dos subconjuntos:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
Ambos subconjuntos son disjuntos:
$$ B_1 \cap B_2 = \varnothing $$
y su unión reproduce exactamente el conjunto original:
$$ B_1 \cup B_2 = B $$
Además, \( B_1 \) y \( B_2 \) son abiertos en la topología subespacio inducida sobre \( B \).
Por tanto, constituyen una separación de \( B \) en \( X \).
Consideremos ahora un subconjunto conexo de \( B \):
$$ A = (1,2) $$
Dado que \( A \subset B_2 \), el conjunto \( A \) queda contenido por completo en uno de los dos subconjuntos de la separación, tal como afirma el resultado general.
Nota. Si, en cambio, se toma \( A = (-1,1) \), se obtiene que $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Esta situación no puede darse, ya que \( B_1 \) y \( B_2 \) forman una separación de \( B \). Un subconjunto conexo de \( B \) no puede distribuirse entre ambos subconjuntos. Si esto fuera posible, entonces \( A \) admitiría a su vez una separación, lo que contradice el hecho bien conocido de que el intervalo \( (-1,1) \) es conexo. El problema no es que \( (-1,1) \) deje de ser conexo, sino que no puede estar contenido en \( B \) cuando \( B \) está separado de esta manera.
Demostración
Hipótesis
Sean \( A \) y \( B \) subconjuntos de un espacio topológico \( X \).
$$ A \subset X \quad \text{y} \quad B \subset X $$
Supongamos que se cumplen las siguientes condiciones:
- \( A \) es un conjunto conexo
- \( A \subset B \)
- \( B_1 \) y \( B_2 \) forman una separación de \( B \) en \( X \)
Proposición
Bajo estas hipótesis, el conjunto \( A \) está contenido en \( B_1 \) o en \( B_2 \):
$$ A \subset B_1 \quad \text{o} \quad A \subset B_2 $$
Demostración
Por hipótesis, \( B_1 \) y \( B_2 \) forman una separación de \( B \) en \( X \). En particular, se cumplen las siguientes propiedades:
- \( B_1 \cap B_2 = \varnothing \), es decir, \( B_1 \) y \( B_2 \) son disjuntos
- \( B = B_1 \cup B_2 \), es decir, su unión coincide con todo \( B \)
- \( B_1 \) y \( B_2 \) son abiertos en la topología subespacio inducida sobre \( B \)
Supongamos, con el fin de obtener una contradicción, que no se cumple ni \( A \subset B_1 \) ni \( A \subset B_2 \). Es decir, supongamos que \( A \) no está contenido por completo en ninguno de los dos subconjuntos.
$$ A \cap B_1 \neq \varnothing \qquad \text{y} \qquad A \cap B_2 \neq \varnothing $$
Dado que \( A \subset B \), se tiene:
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
Como \( B_1 \) y \( B_2 \) son disjuntos, los conjuntos \( A \cap B_1 \) y \( A \cap B_2 \) también lo son.
Además, puesto que \( B_1 \) y \( B_2 \) son abiertos en \( B \), los conjuntos \( A \cap B_1 \) y \( A \cap B_2 \) son abiertos en la topología subespacio inducida sobre \( A \).
Por consiguiente, \( A \cap B_1 \) y \( A \cap B_2 \) son subconjuntos disjuntos, no vacíos y abiertos de \( A \), y constituyen una separación de \( A \) en \( X \).
Esto contradice la hipótesis de que \( A \) es conexo.
En consecuencia, la suposición inicial es falsa y se obtiene el resultado buscado:
$$ A \subset B_1 \quad \text{o} \quad A \subset B_2 $$
Con esto queda demostrada la proposición.
Y así sucesivamente.