Homeomorfismos en topología

Un homeomorfismo es una transformación dentro de la topología que involucra una función biyectiva y continua, junto con su inversa continua.

Esta capacidad permite transformar un espacio en otro y regresar sin necesidad de "romper" o "pegar".

En palabras más simples, un homeomorfismo te permite cambiar la forma de un espacio a otro de manera suave, sin rasgaduras ni adiciones.

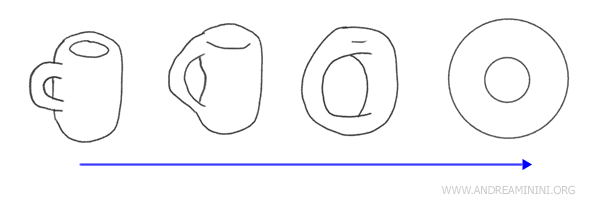
Consideremos, por ejemplo, una taza de café con asa y un donut (toroide); estos se consideran homeomorfos en topología. Esto se debe a que uno puede deformarse continuamente en el otro, y viceversa.

Desde el punto de vista topológico, estas formas son equivalentes porque ambas tienen un único "agujero": el agujero central del donut y el espacio del asa en la taza. Podrías moldear la taza alrededor de su asa para transformarla en un donut.

Cuando dos espacios topológicos están conectados por un homeomorfismo, se les denomina "espacios homeomorfos", indicando que, desde un punto de vista topológico, son fundamentalmente iguales, aunque sus apariencias geométricas sean diferentes.

Características de un homeomorfismo

Estas son algunas de las propiedades fundamentales que definen a un homeomorfismo:

• Función biyectiva
  Establece una correspondencia uno a uno entre los elementos de dos espacios, de modo que cada elemento de un espacio se asocia con uno y solo un elemento del otro, y viceversa.
• Continuidad
  Un homeomorfismo es, por naturaleza, una función continua: pequeñas variaciones en la entrada generan pequeñas variaciones en la salida.
• Función inversa continua
  La función inversa también debe ser continua, lo que garantiza que la transformación pueda revertirse sin perder la continuidad.
• Preservación de propiedades topológicas
  Conserva propiedades topológicas esenciales como la continuidad, la conexidad y la compacidad. En consecuencia, las relaciones internas del espacio original se mantienen intactas en el espacio transformado.

En esencia, un homeomorfismo es una función continua e invertible entre dos espacios topológicos \(X\) y \(Y\), cuya inversa también es continua. Gracias a ello, se preservan las propiedades topológicas de ambos espacios.

Dicho de forma sencilla, un homeomorfismo es una manera de “reconfigurar” un espacio en otro sin desgarrarlo ni pegar sus partes. Es una especie de “equivalencia perfecta” entre dos formas o espacios.

Conviene recordar la definición de continuidad en topología:

Dados dos espacios topológicos \(X\) y \(Y\), una función \(f: X \to Y\) se considera continua si, para todo conjunto abierto \(V\) de \(Y\), la preimagen \(f^{-1}(V)\) es un conjunto abierto en \(X\).

En otras palabras, una función continua en topología conserva la estructura de los conjuntos abiertos al trasladar puntos de un espacio al otro.

Por tanto, la noción de continuidad en topología es más abstracta y general que la empleada en análisis matemático.

Nota: En análisis matemático, la continuidad se define en función de la distancia entre puntos. En topología, en cambio, se basa en la estructura de los conjuntos abiertos, sin necesidad de introducir una noción de distancia.

Un ejemplo práctico

Veamos cómo se pueden ilustrar los conceptos de homeomorfismo y continuidad mediante conjuntos abiertos de manera clara y sencilla.

Consideremos dos espacios topológicos: \(X = \{a, b, c, d\}\) y \(Y = \{1, 2\}\).

• En el espacio \(X\), los conjuntos abiertos son: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• En el espacio \(Y\), los conjuntos abiertos son: \(\{\}, \{1\}, \{1, 2\}\).

Una función \(f: X \rightarrow Y\) es continua si, para cada conjunto abierto en \(Y\), su preimagen es un conjunto abierto en \(X\).

Definamos la función \(f: X \rightarrow Y\) de la siguiente manera:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Para facilitar la comprensión, representaremos la función \(f\) y los espacios topológicos encerrando los conjuntos abiertos en círculos.

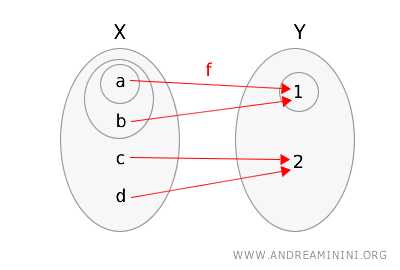
Comprobemos si se cumple la definición de continuidad topológica.

• Si tomamos el conjunto abierto \(\{1\}\) en \(Y\), su preimagen es \(f^{-1}(\{1\}) = \{a, b\}\), que es un conjunto abierto en \(X\).
• Si tomamos el conjunto abierto \(\{1, 2\}\) en \(Y\), su preimagen es \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\), que también es abierto en \(X\).

Como la preimagen de todo conjunto abierto de \(Y\) es un conjunto abierto en \(X\), esta función es continua.

Nota: No se considera el conjunto vacío, ya que por definición es abierto en cualquier espacio topológico.

Analicemos ahora qué ocurre con otra función \(g: X \rightarrow Y\) definida así:

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

También en este caso representaremos la función \(g\) y los espacios topológicos encerrando los conjuntos abiertos en círculos.

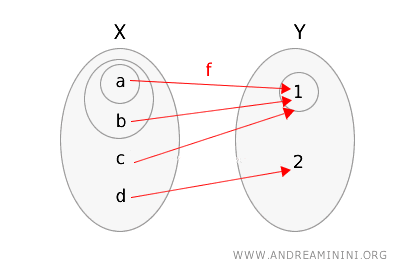
Veamos si cumple con la definición de continuidad topológica.

• Si tomamos el conjunto abierto \(\{1\}\) en \(Y\), su preimagen es \(g^{-1}(\{1\}) = \{a, b, c\}\), que no es un conjunto abierto en \(X\).

Como existe al menos un conjunto abierto en \(Y\) cuya preimagen no es abierta en \(X\), la función \(g\) no es continua.

Nota: En resumen, una función es continua si, para cada conjunto abierto en el espacio de llegada (\(Y\)), su preimagen en \(X\) también es abierta. En el primer caso, la función \(f\) es continua porque esta condición se cumple siempre. En cambio, la función \(g\) no lo es, ya que no se cumple para todos los conjuntos abiertos.

Definición de homeomorfismo

Sean dos espacios topológicos \( X \) y \( Y \), y una función biyectiva \( f: X \to Y \) con inversa \( f^{-1}: Y \to X \). Si tanto \( f \) como \( f^{-1} \) son continuas, entonces \( f \) se denomina un homeomorfismo, y se dice que los espacios \( X \) y \( Y \) son homeomorfos, es decir, \( X \cong Y \).

Los espacios homeomorfos también se conocen como equivalentes topológicos.

¿Qué implica esto?

Que dos espacios sean homeomorfos o topológicamente equivalentes significa que, desde el punto de vista topológico, comparten la misma estructura esencial, aunque sus formas geométricas puedan diferir.

La definición de homeomorfismo se basa en tres condiciones fundamentales:

1. Biyectividad: La función \( f: X \to Y \) debe ser uno a uno y sobre. Es decir, cada punto de \( X \) se asocia de forma única con un punto de \( Y \), y viceversa.
2. Continuidad de \( f \): La función \( f \) es continua si la preimagen de todo conjunto abierto en \( Y \) es un conjunto abierto en \( X \).
3. Continuidad de \( f^{-1} \): La función inversa \( f^{-1}: Y \to X \) también debe ser continua, es decir, la preimagen de cada conjunto abierto en \( X \) bajo \( f \) debe ser abierta en \( Y \).

Ejemplo: Imagina una hoja de papel que se enrolla formando un cilindro. El cilindro y la hoja plana son homeomorfos, ya que se puede pasar de uno al otro sin cortar ni pegar partes, simplemente desenrollando o enrollando. Aunque la forma geométrica cambia, la estructura topológica (es decir, los conjuntos abiertos) permanece inalterada.

Conviene subrayar que el hecho de que una función biyectiva \( f \) sea continua no garantiza que su inversa \( f^{-1} \) también lo sea, a menos que \( f \) sea además una aplicación abierta.

En otras palabras, una función continua y biyectiva no es necesariamente un homeomorfismo si su inversa no es continua.

En topología, una función \( f: X \rightarrow Y \) se considera continua cuando la preimagen de cualquier conjunto abierto en \( Y \) es abierta en \( X \).

No obstante, esto no implica que la imagen de un conjunto abierto en \( X \) sea abierta en \( Y \).

Para que \( f^{-1} \) sea continua, es necesario que \( f \) sea no solo continua y biyectiva, sino también una aplicación abierta.

Ejemplo

Veamos un caso concreto con los siguientes espacios topológicos:

• \( X = (a, b) \) con la topología \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) con la topología \( T_Y = \{\emptyset, Y\} \).

Definimos una función \( f: X \to Y \) tal que \( f(a) = 1 \) y \( f(b) = 2 \).

La función \( f \) es claramente biyectiva: cada elemento de \( X \) se corresponde con un único elemento de \( Y \), y viceversa.

Nota: En el diagrama, los conjuntos abiertos aparecen representados con círculos. En \( X \), los conjuntos \{a\}, \{b\} y \{a, b\} son abiertos; en \( Y \), solo \{1, 2\} es abierto. Los conjuntos vacíos son abiertos por definición, pero se omiten por simplicidad.

Analicemos ahora la continuidad de \( f \) y de su inversa \( f^{-1} \).

• Continuidad de \( f \)
  Para que \( f \) sea continua, la preimagen de cada conjunto abierto de \( Y \) debe ser abierta en \( X \). Como \( T_Y = \{\emptyset, Y\} \), tenemos:
  • \( f^{-1}(\emptyset) = \emptyset \), que es abierto en \( T_X \)
  • \( f^{-1}(Y) = X \), también abierto en \( T_X \)
  Por tanto, \( f \) es continua.
• Continuidad de \( f^{-1} \)
  Consideramos ahora la inversa \( f^{-1}: Y \to X \), con \( f^{-1}(1) = a \) y \( f^{-1}(2) = b \). Analicemos la preimagen de los conjuntos abiertos de \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), abierto en \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), que no es abierto en \( T_Y \)
  • \( f^{-1}(\{b\}) = \{2\} \), tampoco abierto en \( T_Y \)
  • \( f^{-1}(X) = Y \), que sí es abierto en \( T_Y \)
  Dado que algunas preimágenes no son abiertas, \( f^{-1} \) no es continua.

En resumen, aunque \( f \) es biyectiva y continua, su inversa no lo es, por lo que \( f \) no es un homeomorfismo.

Este ejemplo muestra que la continuidad de una función y su biyectividad no bastan para garantizar la continuidad de su inversa.

Nota: La falta de continuidad de \( f^{-1} \) se debe a la diferencia entre las topologías: \( X \) tiene conjuntos abiertos más finos (más “detallados”) que \( Y \), cuya topología es más tosca (solo tiene \( \emptyset \) y \( Y \)).

Ejemplo 2

Veamos ahora otro ejemplo con diferentes topologías:

• \( X = (a, b) \) con \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) con \( T_Y = \{\emptyset, \{1\}, Y\} \).

Definimos \( f: X \to Y \) tal que \( f(a) = 1 \), \( f(b) = 2 \).

La función \( f \) es, nuevamente, biyectiva.

Veamos ahora si \( f \) y \( f^{-1} \) son continuas.

• Continuidad de \( f \)
  Los conjuntos abiertos de \( Y \) son \( \emptyset \), \(\{1\}\) y \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), abierto en \( T_X \)
  • \( f^{-1}(\{1\}) = \{a\} \), abierto en \( T_X \)
  • \( f^{-1}(Y) = X \), abierto en \( T_X \)
  Como todas las preimágenes son abiertas, \( f \) es continua.
• Continuidad de \( f^{-1} \)
  Los conjuntos abiertos de \( X \) son \( \emptyset \), \(\{a\}\) y \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), abierto en \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), abierto en \( T_Y \)
  • \( f^{-1}(X) = Y \), también abierto en \( T_Y \)
  En este caso, \( f^{-1} \) también es continua.

Por lo tanto, \( f \) es biyectiva, continua, y su inversa también lo es. Podemos concluir que \( f \) es un homeomorfismo.

La diferencia con el ejemplo anterior reside en la elección de las topologías, que ahora están mejor ajustadas entre sí.

Nota: Este ejemplo ilustra cómo, al seleccionar adecuadamente las topologías sobre \( X \) y \( Y \), es posible garantizar la continuidad de la inversa y, por tanto, la existencia de un homeomorfismo.

Diferenciación entre homeomorfismos y otras transformaciones topológicas

Aunque el término «homeomorfismo» se emplea en ocasiones de manera amplia para referirse a las transformaciones topológicas, en rigor, designa una clase específica dentro de este conjunto.

Los homeomorfismos y las transformaciones topológicas están estrechamente relacionados, pero no son conceptos equivalentes:

• Transformaciones topológicas
  Constituyen una categoría general que incluye cualquier transformación de un espacio topológico que preserve ciertas propiedades fundamentales, como la continuidad y la conexidad. Entre ellas se encuentran los homeomorfismos, pero también otras transformaciones relevantes como las isotopías, homotopías y difeomorfismos.
• Homeomorfismos
  Se trata de transformaciones que son simultáneamente biyectivas y continuas, cuya inversa también es continua. Permiten establecer una correspondencia reversible entre dos espacios, preservando íntegramente su estructura topológica. Dos espacios relacionados por un homeomorfismo se consideran topológicamente indistinguibles, aunque puedan diferir desde el punto de vista geométrico.

En resumen, aunque todo homeomorfismo es una transformación topológica, no toda transformación topológica cumple los requisitos necesarios para ser un homeomorfismo.

Algunas transformaciones, aunque respeten propiedades topológicas, presentan características particulares o restricciones que las excluyen de la definición estricta de homeomorfismo.

Notas complementarias

A continuación se presentan algunas consideraciones adicionales sobre los homeomorfismos:

• Propiedad topológica
  Una propiedad topológica es una característica intrínseca de un espacio que permanece invariante bajo un homeomorfismo. Es decir, si dos espacios son homeomorfos (existe entre ellos una aplicación continua, biyectiva y con inversa continua), entonces comparten exactamente las mismas propiedades topológicas.
• Teorema de Hausdorff sobre homeomorfismos
  Este teorema establece que si \( f: X \to Y \) es un homeomorfismo y \( X \) es un espacio de Hausdorff, entonces \( Y \) también lo será. Dicho de otro modo, como los homeomorfismos preservan las propiedades topológicas, la separación de puntos característica del espacio de Hausdorff se transmite de \( X \) a \( Y \).
• El análogo del concepto de homeomorfismo en álgebra abstracta es el isomorfismo de grupos. Mientras que un isomorfismo preserva la estructura algebraica de las operaciones, un homeomorfismo conserva la estructura topológica, es decir, la organización de los conjuntos abiertos del espacio.

Y así sucesivamente.