Espacios Regulares en Topología
Un espacio topológico \( X \) se dice regular si satisface las siguientes condiciones:
- Los conjuntos unipuntuales son cerrados, es decir, para cada \( x \in X \), el conjunto \(\{x\}\) es cerrado en \( X \).
- Separación de puntos y conjuntos cerrados: Dados un punto \( a \in X \) y un conjunto cerrado \( C \subset X \) que no lo contiene, existen dos conjuntos abiertos disjuntos \( U \) y \( V \) tales que: \[ a \in U, \quad C \subset V, \quad U \cap V = \emptyset. \]
En topología, la regularidad implica una propiedad de separación más fuerte que la de un espacio de Hausdorff.
Si un espacio es regular y posee una base numerable, el teorema de Urysohn garantiza que es metrizable.
Relación con los espacios de Hausdorff
Los espacios regulares aseguran que un punto y un conjunto cerrado disjunto puedan separarse mediante abiertos disjuntos, lo que representa una condición más exigente que en los espacios de Hausdorff, donde solo se requiere que puntos distintos puedan separarse por abiertos disjuntos.
Nota. No debe confundirse un espacio regular con un espacio normal. La normalidad impone una condición aún más fuerte: cualquier par de conjuntos cerrados disjuntos deben poder separarse mediante abiertos disjuntos. En consecuencia, todo espacio normal es regular, pero no todo espacio regular es normal.
Es importante destacar que la regularidad es solo una de las diversas propiedades de separación. Un espacio topológico puede ser regular sin ser de Hausdorff o viceversa. De hecho, existen ejemplos tanto de espacios de Hausdorff que no son regulares como de espacios regulares que no cumplen la propiedad de Hausdorff.
Ejemplo Práctico
Un caso típico de espacio regular es la recta real \( \mathbb{R} \) con la topología estándar.
Consideremos un punto \( x \in \mathbb{R} \) y un conjunto cerrado \( C \) que no lo contiene.
Por ejemplo, tomemos \( x = 2 \) y el conjunto cerrado \( C \):
\[ C = (-\infty, 0] \cup [5, \infty) \]
Es evidente que \( x = 2 \notin C \) y que \( C \) es cerrado en la topología usual de \( \mathbb{R} \).

Para demostrar la regularidad, necesitamos encontrar abiertos que separen \( x \) de \( C \).
El complemento de \( C \) es un conjunto abierto, lo que nos permite encontrar un intervalo abierto que contenga a \( x \).
Por ejemplo, el intervalo \( (0,5) \) es un entorno de \( x=2 \):
\[ (a, b) = (0, 5) \]
Ahora, elegimos dos valores \( c \) y \( d \) que encierren a \( x = 2 \):
\[ 0 < c < 2 < d < 5 \]
Podemos tomar, por ejemplo, \( c = 1 \) y \( d = 3 \).
Definimos entonces los siguientes conjuntos abiertos:
- \( U = (c, d) = (1,3) \), que es un entorno de \( x = 2 \).
- \( V = (-\infty, c) \cup (d, \infty) = (-\infty, 1) \cup (3, \infty) \), que contiene completamente a \( C \).
Dado que \( U \cap V = \emptyset \), los conjuntos \( U \) y \( V \) cumplen la condición de separación requerida para la regularidad.
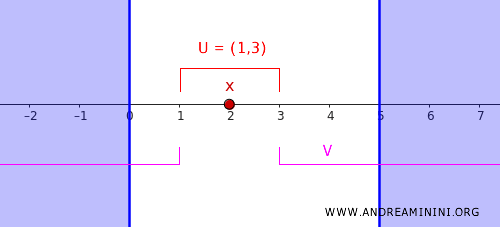
En conclusión, hemos logrado separar el punto \( x = 2 \) del conjunto cerrado \( C \) mediante dos abiertos disjuntos \( U \) y \( V \), lo que confirma que \( \mathbb{R} \) con la topología estándar es un espacio regular.
Notas
Algunas ideas para entender mejor los espacios regulares
- Los axiomas de separación
En topología, conceptos como Hausdorff y regular pertenecen a un conjunto de principios conocidos como los axiomas de separación. Estos axiomas explican hasta qué punto un espacio puede diferenciar puntos y conjuntos mediante vecindades abiertas que no se superponen. Comprenderlos nos ayuda a ver qué tan "precisa" es una topología a la hora de distinguir entre los distintos elementos de un espacio.Nota. De forma intuitiva, un espacio es Hausdorff cuando podemos encerrar dos puntos distintos en conjuntos abiertos separados, sin que se toquen. En cambio, un espacio es regular cuando también podemos separar un punto de un conjunto cerrado que no lo contiene, usando el mismo criterio. Estas propiedades muestran la capacidad de un espacio para diferenciar con claridad sus elementos, algo así como su nivel de "resolución topológica".
Y así sucesivamente.