Topología Cociente

Sea $X$ un espacio topológico y $A$ un conjunto que no necesariamente es un subconjunto de $X$. Supongamos que $p: X \rightarrow A$ es una aplicación suprayectiva. Un subconjunto $U$ de $A$ se dice abierto si, y solo si, $p^{-1}(U)$ es abierto en $X$.

En otras palabras, un conjunto $U$ de $A$ es abierto en la topología cociente si, y solo si, su preimagen $p^{-1}(U)$ - es decir, el conjunto de los puntos de $X$ que se envían a $U$ mediante $p$ - es abierto en $X$.

ilustración de topología cociente

Este concepto permite definir una nueva topología en $A$, denominada topología cociente, a partir de la topología de $X$ a través de la aplicación $p$.

Al conjunto $A$ se le conoce como espacio cociente y a la función $p$ como la aplicación cociente.

La colección de abiertos en $A$ suele describirse como la "topología cociente inducida por $p$."

En resumen, en la topología cociente, un conjunto se considera abierto si su preimagen en el espacio original es abierta.

Conviene aclarar un error frecuente:

La preimagen de un abierto en el espacio cociente $A$ es abierta en $X$, pero el recíproco no necesariamente se cumple.
La imagen de un abierto de $X$ no tiene por qué ser abierta en $A$, ya que la aplicación $p$ puede alterar su estructura.

En definitiva, un espacio cociente es un espacio topológico que se obtiene a partir de otro identificando, o "pegando", determinados puntos según una relación de equivalencia.

De manera sencilla, un espacio cociente surge al "fusionar" puntos de un espacio conforme a una regla dada, y estudiar luego las propiedades topológicas del nuevo espacio.

¿Por qué es útil la topología cociente? Gracias a la topología cociente, podemos analizar el comportamiento de un espacio $A$ más complejo, aprovechando el conocimiento que tenemos sobre $X$, que en general resulta más sencillo de manejar.

Explicación
Un ejemplo práctico
Propiedades de la Topología Cociente

Explicación

El concepto de "topología cociente" puede resultar abstracto al principio, pero vamos a tratar de entenderlo de forma intuitiva.

La topología cociente es una manera de transformar una figura pegando entre sí algunos de sus bordes o caras.

Imagina, por ejemplo, que tienes una hoja cuadrada de papel. Si pegas dos lados opuestos, obtienes un cilindro.

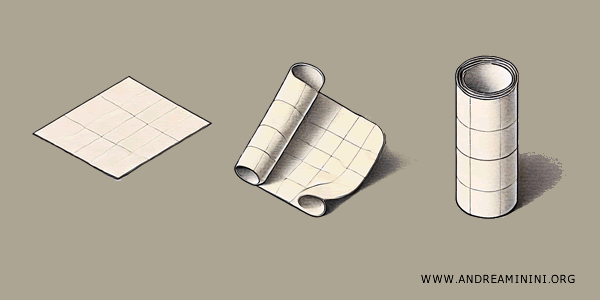
plegado de una hoja para formar un cilindro

Si después unes los bordes circulares del cilindro, formas una rosquilla o toro.

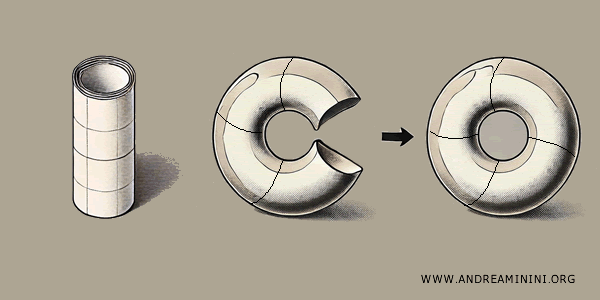
ejemplo de toro generado a partir de un cilindro

En este proceso, el cuadrado primero se convierte en un cilindro y luego en un toro al pegar adecuadamente sus bordes.

Del mismo modo, la topología cociente nos permite construir nuevos espacios topológicos a partir de espacios más simples, identificando partes específicas.

Este enfoque es fundamental en matemáticas para estudiar de manera abstracta las propiedades de superficies y espacios.

Un ejemplo práctico

Consideremos el espacio topológico $ X = [0, 1] $ con la topología usual, donde los abiertos son intervalos abiertos o uniones de intervalos abiertos.

En este espacio se cumple que:

El conjunto $ X $ y el conjunto vacío $ \emptyset $ son abiertos por definición.
Cualquier intervalo abierto $ (a,b) $ con $ 0 \leq a < b \leq 1 $ es abierto en $X$.

Podemos imaginar el espacio $ X $ como un segmento de recta con extremos en $0$ y $1$.

representación gráfica del segmento [0,1]

Ahora vamos a construir un nuevo espacio cociente identificando los puntos $0$ y $1$ del intervalo $[0, 1]$, es decir, considerándolos como un único punto.

Definimos entonces una aplicación $ p: [0, 1] \rightarrow A $ de la siguiente forma:

$$ p(x) = \begin{cases} p(0) & \text{si } x = 0 \text{ o } x = 1 \\ \\ x & \text{si } 0 < x < 1 \end{cases} $$

El conjunto cociente $A$ que obtenemos puede visualizarse como un círculo, en el que $0$ y $1$ han sido identificados.

formación de un círculo mediante topología cociente

En otras palabras, hemos "curvado" el segmento para unir sus extremos y formar una figura cerrada.

En el nuevo espacio $A$, el punto $P = \{0,1\}$ representa la imagen de ambos extremos bajo la aplicación $p$.

Para definir la topología en $A$, debemos determinar qué subconjuntos serán considerados abiertos.

Por definición, un conjunto $U \subseteq A$ será abierto si su preimagen $p^{-1}(U)$ es un abierto de $[0,1]$.

Veamos dos situaciones:

Intervalo $ U = (a,b) $ que no contiene a $P$
Su preimagen en $X$ es el intervalo abierto $ (a,b) $, por lo que $U$ es abierto en $A$.
Intervalo $ U = (a,b) $ que contiene a $P = \{0,1\}$
La preimagen en $X$ es la unión de dos intervalos $ [0,a) \cup (b,1] $, ambos abiertos en $X$. Así, $U$ es abierto en $A$.

De esta forma, hemos construido un nuevo espacio topológico $A$ - un círculo - a partir del intervalo $[0,1]$.

Este es un ejemplo clásico de cómo la topología cociente puede transformar un espacio sencillo en uno mucho más interesante.

Ejemplo 2

En este ejemplo de topología cociente, queremos "enrollar" la recta real sobre un círculo.

Consideremos la recta real ($ \mathbb{R} $), que se extiende infinitamente en ambas direcciones.

La idea es "envolver" la recta alrededor de un círculo identificando cada número real con su parte fraccionaria.

Para ello, definimos la aplicación $ p(x) = x \mod 1 $.

¿Qué significa esto? De manera sencilla: a cada número real $x$, le asociamos únicamente su parte decimal (es decir, la parte que queda después del punto decimal) para representarlo en el círculo.

Por ejemplo, si $ x = 1{,}3 $, tomamos su parte decimal, 0,3, y la ubicamos en un punto del círculo. Si $ x = 2{,}7 $, la parte decimal es 0,7, por lo que corresponde al mismo punto que $0{,}7$.
enrollado de la recta real sobre un círculo

Observamos que, cada vez que $x$ aumenta en una unidad entera (por ejemplo, de 1,3 a 2,3 o a 3,3), el punto se proyecta en el mismo lugar del círculo.

Esta operación de "enrollar" la recta real consiste en hacer coincidir los puntos 0 y 1, y por tanto todos sus equivalentes.

Analicemos ahora algunos intervalos concretos.

Intervalo (0,1) en $ \mathbb{R} $
El intervalo $ (0, 1) $ se enrolla formando un arco del círculo, sin incluir el punto 0. Este intervalo es abierto en el espacio cociente, ya que su preimagen en $ \mathbb{R} $ también es abierta.
Intervalo (1,2) en $ \mathbb{R} $
El intervalo $ (1,2) $ se proyecta exactamente en el mismo arco que $ (0,1) $, ya que $1 \mod 1 = 0$ y $2 \mod 1 = 0$. Así, no aporta información nueva respecto a la topología cociente.
Intervalo (0,2) en $ \mathbb{R} $
El intervalo $ (0,2) $ cubre toda la circunferencia, pasando dos veces por cada punto. Aunque $ (0,2) $ sea abierto en $ \mathbb{R} $, su imagen en el círculo es todo el espacio, que en este caso resulta ser un conjunto abierto y cerrado (clopen), ya que un círculo no posee borde.

Nota: Este ejemplo ilustra que un conjunto abierto en el espacio original no necesariamente se proyecta como un abierto en el espacio cociente.

En cambio, siempre que consideremos un abierto en el círculo, su preimagen en $ \mathbb{R} $ será abierta.

Esto sucede porque al "desenrollar" un conjunto abierto del círculo hacia $ \mathbb{R} $, obtenemos una unión de intervalos abiertos.

Sin embargo, el recíproco no es cierto: no todo abierto en $ \mathbb{R} $ tendrá necesariamente una imagen abierta en el círculo.

Conclusión

No podemos asumir que un conjunto abierto de $ \mathbb{R} $ se proyecte como un abierto en el círculo, ya que la aplicación de enrollado puede distorsionar la estructura de los conjuntos.

Ejemplo 3

En este ejercicio construiremos una topología cociente a partir de una sucesión de enteros consecutivos, uniendo el primer ($m$) y el último ($n$) elementos de la secuencia $ \{ m, m+1, \ldots, n \} $ tomada de $ \mathbb{Z} $.

Consideremos la sucesión de 7 enteros consecutivos del 1 al 7:

$$ I_7 = \{1, 2, 3, 4, 5, 6, 7\} $$

Este conjunto constituye un intervalo digital, ya que incluye números enteros consecutivos.

Unimos ahora el primer número (1) con el último (7), como si cerráramos una línea recta para formar un lazo o círculo.

creación de un círculo digital a partir de un intervalo

De esta manera obtenemos una nueva estructura, denominada círculo digital $ C_6 $, compuesto por 6 puntos.

En este círculo, cada punto es adyacente exactamente a dos vecinos.

Este es un caso de topología cociente, ya que hemos modificado la estructura original para formar un nuevo espacio topológico.

Nota: El resultado es similar al círculo obtenido al identificar los extremos de un intervalo real $(a,b)$, aunque aquí trabajamos con enteros, dando lugar a un conjunto finito.

El círculo digital constituye también un ejemplo de topología digital, donde cada punto está conectado a sus vecinos inmediatos.

Se trata de un espacio discreto, en el que se aplican conceptos como conectividad y abiertos digitales.

Nota: En topología digital, un conjunto $ U $ se considera abierto si, para cada punto $ x \in U $, sus vecinos también pertenecen a $ U $, según la conexión adoptada (conexión-2 en 1D, conexión-4 o conexión-8 en 2D, o conexión-6 o conexión-18 en 3D).

Es fundamental destacar que la topología cociente y la topología digital son nociones distintas.

En otras palabras, aunque el círculo digital pueda obtenerse mediante una identificación de puntos, pertenece a una categoría diferente dentro de la topología discreta.

Ejemplo 4

Consideremos el conjunto de los números reales $ \mathbb{R} $ con su topología estándar, y definamos una aplicación cociente $ p: \mathbb{R} \to \{a, b, c\} $ de la siguiente forma:

$$ p(x) = \begin{cases} a \quad \text{si} \quad x < 0 \\ \\ b \quad \text{si} \quad x = 0 \\ \\ c \quad \text{si} \quad x > 0 \\ \\ \end{cases} $$

En esencia, esta aplicación "colapsa" todo el subconjunto de números negativos en el punto $ a $, el número $ 0 $ en el punto $ b $, y el conjunto de números positivos en el punto $ c $.

La topología cociente inducida por esta aplicación se determina a partir de las preimágenes de $ a $, $ b $ y $ c $.

Estas preimágenes son:

$ p^{-1}(a) = (-\infty, 0) $, que es un conjunto abierto en $ \mathbb{R} $,
$ p^{-1}(b) = \{0\} $, que no es abierto en $ \mathbb{R} $,
$ p^{-1}(c) = (0, \infty) $, que es abierto en $ \mathbb{R} $.

Recordemos que en la topología cociente un conjunto de $ \{a, b, c\} $ será abierto si, y solo si, su preimagen bajo $ p $ es abierta en $ \mathbb{R} $. Por tanto, podemos concluir que son abiertos en la topología cociente:

El conjunto $ \{a\} $, ya que $ p^{-1}(\{a\}) = (-\infty, 0) $ es abierto en $ \mathbb{R} $.
El conjunto $ \{c\} $, pues $ p^{-1}(\{c\}) = (0, \infty) $ es abierto en $ \mathbb{R} $.
La unión $ \{a, c\} $, cuya preimagen es $ (-\infty, 0) \cup (0, \infty) = \mathbb{R} \setminus \{0\} $, también abierta en $ \mathbb{R} $.

Asimismo, tanto el conjunto total como el conjunto vacío son abiertos en la topología cociente:

El conjunto total $ \{a, b, c\} $ es abierto porque su preimagen es todo $ \mathbb{R} $, abierto en su topología estándar.
El conjunto vacío $ \emptyset $ es abierto, ya que su preimagen sigue siendo $ \emptyset $, que es abierto en cualquier topología.

Por el contrario, el conjunto $ \{b\} $ no es abierto en la topología cociente, puesto que su preimagen $ \{0\} $ no es abierta en $ \mathbb{R} $.

En conclusión, los conjuntos abiertos en la topología cociente sobre $ \{a, b, c\} $ son $ \emptyset $, $ \{a\} $, $ \{c\} $, $ \{a, c\} $ y $ \{a, b, c\} $, mientras que $ \{b\} $ no es abierto, dado que el punto $ 0 $ no constituye un abierto en $ \mathbb{R} $.

En otras palabras, $ b $ actúa como una "singularidad", un punto aislado que no puede formar parte de ningún abierto no trivial en esta topología.

Propiedades de la Topología Cociente

A continuación, resumimos algunas propiedades fundamentales de la topología cociente:

El conjunto vacío y el conjunto total son siempre abiertos
En toda topología cociente, tanto el conjunto vacío como el conjunto total son abiertos.
- Preimagen del conjunto vacío
  La preimagen de $ \emptyset $ bajo $ p $ es $ \emptyset $ en $ X $, que es abierto. Por tanto, $ \emptyset $ es abierto en la topología cociente.
- Preimagen del conjunto total
  La preimagen del conjunto total $ A $ bajo $ p $ es $ X $, que también es abierto en $ X $.
Nota: Esto implica que las operaciones triviales - el conjunto vacío y el conjunto total - siempre se preservan como abiertos en cualquier topología, incluida la topología cociente.
Uniones arbitrarias de abiertos
Si cada $ U_i $ es abierto en la topología cociente de $ A $, entonces la unión de estos conjuntos sigue siendo abierta:
$$ \left( \forall i, \ U_i \text{ abierto en } A \right) \Rightarrow p^{-1}\left( \bigcup U_i \right) = \bigcup p^{-1}(U_i) \text{ abierto en } X. $$
Nota: Dado que la unión de abiertos es abierta en $ X $, la propiedad se preserva en $ A $. Es decir, la apertura es estable bajo uniones arbitrarias en la topología cociente.
Intersecciones finitas de abiertos
Si los conjuntos $ U_i $ son abiertos en $ A $, entonces la intersección finita de sus preimágenes sigue siendo abierta en $ X $.
Nota: Cada $ p^{-1}(U_i) $ es abierto en $ X $, y como la intersección finita de abiertos es abierta, también lo será $ \bigcap p^{-1}(U_i) $. Esto garantiza que la intersección de abiertos en $ A $ corresponde a un abierto en $ X $.

Estos principios constituyen la base para comprender el comportamiento de las topologías cocientes.