Subespacio Topológico

Un subespacio topológico es un subconjunto de un espacio topológico que hereda su topología del espacio original.

Sea \( (X, T) \) un espacio topológico, donde \( X \) es un conjunto y \( T \) es una colección de conjuntos abiertos que define la topología en \( X \). Sea \( Y \) un subconjunto de \( X \). La topología de subespacio en \( Y \) se define como: \[ T_Y = \{ U \cap Y \mid U \in T \} \]

En otras palabras, un conjunto \( V \subseteq Y \) se considera abierto en la topología de subespacio si puede expresarse como la intersección de \( Y \) con un conjunto abierto \( U \) en el espacio original \( X \).

Así, todos los conjuntos abiertos en la topología de subespacio \( Y \) son de la forma \( U \cap Y \), donde \( U \) es abierto en \( X \).

$$ V_{open \ in \ Y} = U \cap Y $$

De igual manera, todos los conjuntos cerrados en la topología de subespacio \( Y \) son de la forma \( C \cap Y \), donde \( C \) es cerrado en \( X \).

$$ V_{closed \ in \ Y} = C \cap Y $$

Nota. Los conjuntos abiertos en la topología de subespacio \( Y \) pueden no ser abiertos en el espacio topológico \( X \). En general, puede haber conjuntos que sean abiertos en \( Y \) pero cerrados en \( X \), o viceversa. Además, algunos conjuntos pueden ser abiertos o cerrados tanto en \( Y \) como en \( X \). Y, por supuesto, también pueden existir conjuntos "clopen", que son a la vez abiertos y cerrados. En el primer ejemplo de estas notas, se demuestra un caso de este tipo y se explica por qué ocurre.

Ejemplo Práctico

Consideremos el espacio topológico \( \mathbb{R} \) con la topología estándar, donde los conjuntos abiertos son intervalos abiertos.

Sea \( Y = [0, 1] \) un subconjunto de \( \mathbb{R} \).

La topología de subespacio en \( Y \) incluye conjuntos de la forma:

$$ U \cap [0, 1] $$

donde \( U \) es un conjunto abierto en \( \mathbb{R} \).

Por ejemplo, el conjunto (-1, 0.5) es abierto en el espacio topológico \( \mathbb{R} \).

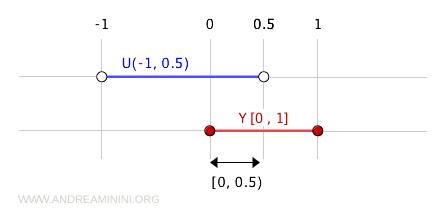
La intersección de (-1, 0.5) con el conjunto \( Y = [0, 1] \) es un conjunto abierto en la topología de subespacio en \( Y \).

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

Por lo tanto, el conjunto \( [0, 0.5) \) es abierto en el subespacio \( Y \).

Por otro lado, el conjunto \( [0, 0.5] \) es cerrado en la topología de subespacio sobre \( Y \) porque se puede obtener al intersectar el conjunto cerrado [-1, 0.5] en \( X \) con el conjunto \( Y \).

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

En resumen, el subespacio topológico \( Y \) hereda una estructura topológica del espacio original \( X \) de tal manera que los conjuntos abiertos en \( Y \) son intersecciones de \( Y \) con los conjuntos abiertos de \( X \).

Nota. Conjuntos como [0,a) o (a,1], donde 0<a<1, son cerrados en la topología estándar en \( \mathbb{R} \), pero son abiertos en la topología de subespacio porque se pueden obtener como intersecciones entre \( Y = [0,1] \) y un conjunto abierto en \( \mathbb{R} \). Por ejemplo, consideremos el conjunto abierto (-1,0.5) en \( \mathbb{R} \) y su intersección con \( Y = [0,1] \): $$ (-1,0.5) \cap [0,1] = [0,0.5) $$ El intervalo [0,0.5) es abierto en el subespacio \( Y \) aunque no sea abierto en la topología estándar sobre \( \mathbb{R} \).

Es importante destacar que existen conjuntos que son abiertos tanto en la topología de subespacio \( Y \) como en \( X \). Por ejemplo, el conjunto (0.2, 0.8).

También hay conjuntos que son cerrados tanto en la topología \( Y \) como en \( X \), como el conjunto [0.2, 0.8].

Finalmente, en la topología de subespacio \( Y = [0, 1] \), el conjunto \( [0, 1] \) es tanto abierto como cerrado.

• Abierto
  Para demostrar que \( [0, 1] \) es abierto en el subespacio \( Y \), necesitamos encontrar un conjunto abierto \( U \) en \( \mathbb{R} \) tal que \( U \cap Y = [0, 1] \). Podemos simplemente elegir \( U = \mathbb{R} \), que es obviamente abierto en \( \mathbb{R} \). Entonces: $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Por lo tanto, \( [0, 1] \) es abierto en el subespacio \( Y \).
• Cerrado
  Para demostrar que \( [0, 1] \) es cerrado en el subespacio \( Y \), necesitamos encontrar un conjunto cerrado \( C \) en \( \mathbb{R} \) tal que \( C \cap Y = [0, 1] \). Podemos tomar \( C = [0, 1] \), que es cerrado en \( \mathbb{R} \). $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ Así, \( [0, 1] \) es cerrado en el subespacio \( Y \).

  Nota: Alternativamente, podemos demostrar que \( [0, 1] \) es cerrado en \( Y \) al notar que el complemento de \( [0, 1] \) en \( Y \) es el conjunto vacío, que es abierto en cualquier topología. Dado que el complemento de un conjunto abierto es cerrado, se sigue que \( [0, 1] \) es cerrado en \( Y \).

En conclusión, el conjunto \( [0, 1] \) en la topología de subespacio \( Y = [0, 1] \) es tanto abierto como cerrado.

Este tipo de conjunto también se conoce como "clopen", una combinación de las palabras "closed" y "open".

Ejemplo 2

Considera la topología estándar en el conjunto de los números reales \( \mathbb{R} \).

En esta topología, cualquier conjunto abierto (a,b) con a>b es un conjunto abierto.

Un subespacio topológico de \( \mathbb{R} \) es el conjunto de números enteros \( \mathbb{Z} \), ya que cada entero se puede obtener como la intersección de intervalos abiertos en el conjunto de números reales.

Por ejemplo, el número entero 7 se puede obtener al intersectar el conjunto abierto (6.5,7.5) en \( \mathbb{R} \) con el conjunto de enteros \( \mathbb{Z} \).

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

De la misma manera, cualquier otro número entero se puede obtener.

Así, cada número entero es un conjunto abierto en el subespacio topológico de \( \mathbb{ Z} \).

Del mismo modo, cualquier subconjunto de \( \mathbb{Z} \) también es un conjunto abierto en este subespacio.

Por ejemplo, para obtener el conjunto {6,7,8}, simplemente se intersecta el conjunto abierto (5.5,8.5) con el conjunto \( \mathbb{Z} \).

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

Este subespacio topológico en \( \mathbb{Z} \) también se conoce como la topología discreta.

Nota: La topología discreta en \( \mathbb{Z} \) no es un subespacio de la topología estándar en \( \mathbb{R} \); más bien, es una topología en sí misma. Sin embargo, la topología de subespacio que \( \mathbb{Z} \) hereda de la topología estándar en \( \mathbb{R} \) es equivalente a la topología discreta en \( \mathbb{Z} \).

Ejemplo 3

Consideremos el espacio euclidiano tridimensional \( \mathbb{R}^3 \) con la topología estándar donde los conjuntos abiertos son uniones de bolas abiertas.

Ahora, consideremos la esfera unitaria \( S^2 \), definida como el conjunto de puntos en \( \mathbb{R}^3 \) que están a una distancia de 1 del origen:

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

La topología de subespacio en \( S^2 \) se define de la siguiente manera:

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ es abierto en } \mathbb{R}^3 \} $$

En otras palabras, un conjunto \( V \subseteq S^2 \) es abierto en la topología de subespacio si y solo si puede escribirse como la intersección de \( S^2 \) con un conjunto abierto \( U \) en \( \mathbb{R}^3 \).

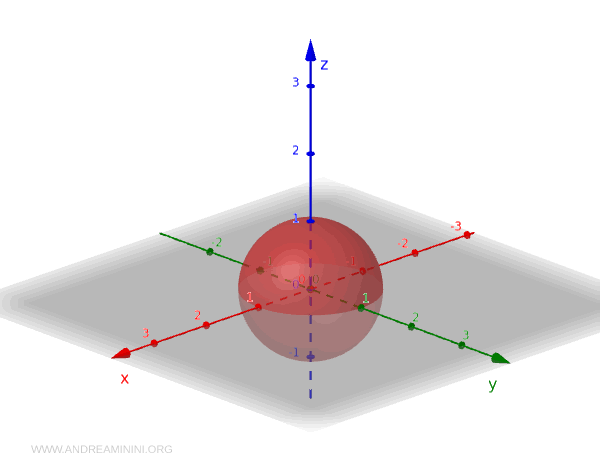
A continuación, se presentan algunos ejemplos de conjuntos abiertos en \( S^2 \):

• Unión de subespacios abiertos en \( \mathbb{R}^3 \)
  Consideremos el conjunto abierto \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} \). La intersección de \( U \) con \( S^2 \) es: $$ U \cap S^2 = S^2 $$ porque cada punto en \( S^2 \) satisface \( x^2 + y^2 + z^2 = 1 \), que es claramente menor que 2. Por lo tanto, \( S^2 \) es abierto en sí mismo.
• Una pequeña porción de la esfera
  Consideremos \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \text{ y } z > 0 \} \. Este \( U \) representa la parte superior de la esfera unitaria (hemisferio superior). La intersección con \( S^2 \) es: $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ Este conjunto representa la parte superior de la esfera y es abierto en la topología de subespacio \( T_{S^2} \).
• Conjuntos abiertos y cierre
  El conjunto vacío \( \emptyset \) y \( S^2 \) en sí son abiertos en \( S^2 \).
  
  • La intersección finita de conjuntos abiertos en \( S^2 \) es abierta en \( S^2 \).
  • La unión arbitraria de conjuntos abiertos en \( S^2 \) es abierta en \( S^2 \).

En resumen, la esfera \( S^2 \) como subespacio topológico de \( \mathbb{R}^3 \) hereda su estructura topológica de la topología estándar de \( \mathbb{R}^3 \), donde los conjuntos abiertos en \( S^2 \) son intersecciones de \( S^2 \) con conjuntos abiertos en \( \mathbb{R}^3 \).

Propiedades de la Topología de Subespacio

A continuación, se presentan las principales propiedades de la topología de subespacio:

1. Conjuntos abiertos
   Los conjuntos abiertos en \( Y \) son todos de la forma \( U \cap Y \), donde \( U \) es abierto en \( X \).
2. Conjuntos vacío y total
   El conjunto vacío \( \emptyset \) y el conjunto \( Y \) en sí siempre son abiertos en \( Y \):
   - \( \emptyset \) es abierto porque \( \emptyset = \emptyset \cap Y \).
   - \( Y \) es abierto porque \( Y = X \cap Y \).
3. Intersecciones finitas
   La intersección de un número finito de conjuntos abiertos en \( Y \) sigue siendo abierta en \( Y \). Si \( V_1, \ldots, V_n \) son abiertos en \( Y \), entonces: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap Y) \cap \cdots \cap (U_n \cap Y) = (U_1 \cap \cdots \cap U_n) \cap Y $$ donde cada \( U_i \) es abierto en \( X \), y la intersección finita de conjuntos abiertos en \( X \) es abierta en \( X \).
4. Uniones arbitrarias
   La unión arbitraria de conjuntos abiertos en \( Y \) sigue siendo abierta en \( Y \). Si \( V_\alpha \) es abierto en \( Y \) para cada \( \alpha \) en algún conjunto índice \( I \), entonces: $$ \bigcup_{\alpha \in I} V_\alpha = \bigcup_{\alpha \in I} (U_\alpha \cap Y) = \left( \bigcup_{\alpha en I} U_\alpha \right) \cap Y $$ donde cada \( U_\alpha \) es abierto en \( X \), y la unión arbitraria de conjuntos abiertos en \( X \) es abierta en \( X \).

Notas

Algunas notas adicionales sobre subespacios:

• La topología estándar en cualquier subespacio \( Y \) de \( \mathbb{R^n} \) es equivalente a la topología de subespacio de \( \mathbb{R^n} \).

  Ejemplo. Consideremos el conjunto \( Y = [-1,0) \cup (0,1] \), que es un subconjunto de \( \mathbb{R} \). En la topología estándar sobre \( Y \), los intervalos [-1,0) y (0,1] son ambos abiertos porque se pueden obtener como intersecciones de \( Y \) con conjuntos abiertos en la topología estándar sobre los números reales \( \mathbb{R} \). Por ejemplo, consideremos los conjuntos abiertos (-1.5,0.5) y (0,1.5) en la topología estándar sobre \( \mathbb{R} \): $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Por lo tanto, la topología estándar sobre \( Y \) es equivalente a la topología de subespacio de la topología estándar sobre \( \mathbb{R} \). En este caso, los intervalos [-1,0) y (0,1] también son cerrados en la topología estándar sobre \( Y \) porque el complemento del conjunto abierto [-1,0) es (0,1], lo que convierte a (0,1] en un conjunto cerrado . De manera similar, el complemento del conjunto abierto (0,1] es [-1,0) en la topología estándar sobre \( Y \), por lo que [-1,0) es un conjunto cerrado. En conclusión, los conjuntos [-1,0) y (0,1] son tanto abiertos como cerrados (clopen) en la topología estándar sobre \( Y \).

• Teorema de la base en la topología de subespacio
  Este teorema afirma que si tenemos una base \( B_X \) para la topología de un espacio topológico \(X\) y consideramos un subconjunto \(Y \subset X \), entonces la colección de conjuntos formada al intersectar \( B \) con \(Y\) constituye una base \( B_Y \) para la topología de subespacio en \(Y\). $$ B_Y = \{ B \cap Y \ | \ B \in B_X \} $$

Y así sucesivamente.