La Base de una Topología

La base de una topología es una colección B de conjuntos abiertos tal que cualquier conjunto abierto del espacio topológico T puede expresarse como una unión de conjuntos pertenecientes a B.

Supongamos que tenemos un conjunto X y una colección T de subconjuntos de X que definen una topología sobre X. En este contexto, una base de la topología T es una colección B de conjuntos, llamados elementos básicos, que cumplen las siguientes condiciones:

• Cada elemento x de X debe pertenecer al menos a un conjunto de B.
• Si x pertenece a la intersección no vacía B₁∩B₂ de dos conjuntos de B, entonces existe otro conjunto B₃ en B, contenido en dicha intersección, que también contiene a x. Es decir, x debe estar contenido en un conjunto básico más pequeño dentro de la intersección.
  

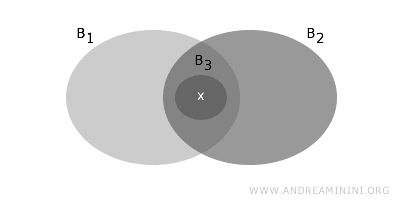
Estas condiciones garantizan que la colección de conjuntos B forme una base para la topología T.

¿Por qué es relevante?

La noción de base es fundamental porque permite describir la topología T mediante un conjunto más manejable de conjuntos básicos, evitando la necesidad de especificar directamente todos los conjuntos abiertos de T.

Nota. La propiedad sobre la intersección de conjuntos básicos garantiza que la topología satisface axiomas esenciales, en particular que la intersección de dos conjuntos abiertos es también un conjunto abierto.

Un Ejemplo Concreto

Consideremos el conjunto

$$ X = \{a, b, c \} $$

y la topología

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

Aquí, T representa la colección de todos los conjuntos abiertos en X, definidos de acuerdo con esta topología.

Una base B para esta topología podría ser:

$$ B = \{ \{ a \}, \{ b,c \} \} $$

Esta elección de base es válida porque cada elemento de X pertenece al menos a un conjunto de B y cualquier conjunto abierto en T puede expresarse como una unión de elementos de B.

Observemos que cualquier conjunto abierto en T se obtiene como unión de elementos de B. Por ejemplo:

• El conjunto {a} ya pertenece a B.
• El conjunto {b, c} también pertenece a B.
• El conjunto {a, b, c} se obtiene como la unión de ambos:
  $$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

Nota. En teoría de conjuntos, el conjunto vacío (Ø) es un subconjunto impropio de cualquier conjunto y, por definición, siempre está incluido. Por lo tanto, también pertenece a la topología: $$ \emptyset \in T $$ Además, en cualquier topología, el conjunto vacío es abierto por definición.

Este ejemplo ilustra el concepto de base en un caso finito. Sin embargo, en contextos más generales, especialmente en espacios infinitos, la construcción de una base puede ser más compleja. Aun así, la idea central sigue siendo la misma: una base proporciona los "bloques de construcción" a partir de los cuales se generan todos los conjuntos abiertos del espacio topológico.

Otro Enfoque

Una base alternativa B para la topología en el conjunto \(X = \{a, b, c\}\) podría ser:

$$ B = \{ \{ a \}, \{ b \}, \{ c \} \} $$

En este caso, la base está formada por los conjuntos unitarios de los elementos de \(X\).

Verifiquemos que \(B\) realmente constituye una base para la topología \(T = \{ \varnothing, X, \{a\}, \{b,c\} \}\):

• El conjunto vacío \( \varnothing \) es abierto por definición y no requiere construcción alguna. Además, es un subconjunto impropio de cualquier conjunto y siempre está presente.
• El conjunto \( \{a\} \) ya pertenece a \( B \). $$ \{ a \} \in B $$
• El conjunto \( \{b,c\} \) puede expresarse como la unión de los conjuntos \( \{b\} \) y \( \{c\} \), ambos en \( B \). $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
• El conjunto total \( X = \{a,b,c\} \) se obtiene como la unión de todos los conjuntos de \( B \): $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

Por lo tanto, \( B \) es efectivamente una base para la topología en \( X \), ya que permite reconstruir todos los conjuntos abiertos de \( T \) mediante uniones de elementos de \( B \).

Nota. Este ejemplo muestra cómo una misma topología puede admitir distintas bases, cada una proporcionando una forma diferente de "generar" sus conjuntos abiertos a partir de uniones de conjuntos básicos.

Ejemplo 2

Consideremos ahora la base estándar para la topología usual en la recta real, que consiste en todos los intervalos abiertos:

$$ B = \{ (a,b) \subseteq \mathbb{R} \mid a < b \} $$

Esta colección de conjuntos forma una base, ya que cualquier punto de la recta real está contenido en algún intervalo abierto \( (a,b) \).

Además, si dos intervalos abiertos se intersecan, la intersección también contiene un intervalo abierto más pequeño, lo que garantiza que la segunda condición de base se cumple.

Por ejemplo, consideremos los intervalos abiertos \( (0,3) \) y \( (2,4) \). Su intersección es el intervalo abierto \( (2,3) \), que pertenece a la base \( B \):

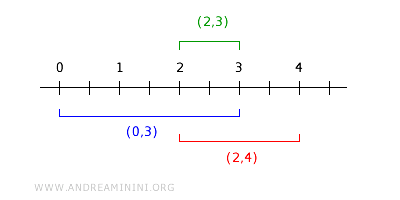
En efecto, el intervalo \( (2,3) \) está completamente contenido en la intersección \( (0,3) \cap (2,4) \), garantizando así la estructura de base: $$ (0,3) \cap (2,4) = (2,3) \in B $$

Observaciones

Algunas observaciones adicionales sobre la base de una topología:

• Si tomamos un conjunto \( X \) y construimos una base \( B \) donde cada elemento \( x \in X \) está contenido en un conjunto unitario \( \{x\} \in B \), podemos generar cualquier topología sobre \( X \).

  En general, la unión de conjuntos unitarios permite generar cualquier topología.
  
  Por ejemplo, la base \( B = \{ \{a\}, \{b\}, \{c\} \} \) para el conjunto \( X = \{a,b,c\} \) genera la topología \( T = \{ \varnothing, \{a\}, \{b,c\}, X \} \).
  
  Sin embargo, la misma base \( B \) también puede generar otras topologías sobre \( X \), como:
  • La topología \( T = \{ \varnothing, \{b\}, \{a,c\}, X \} \).
  • La topología trivial \( T = \{ \varnothing, X \} \).
  • La topología discreta \( T = \{ \varnothing, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, X \} \).

  Nota. La primera condición para ser base se cumple porque cada elemento de \( X \) está contenido en algún conjunto de \( B \). La segunda condición también se satisface, ya que los conjuntos \( \{x\} \) son disjuntos por construcción, al estar formados por un único elemento de \( X \).

Este principio se generaliza a cualquier conjunto y topología.