El Conjunto Vacío

El conjunto vacío es un conjunto que no contiene ningún elemento. Se representa con el símbolo Ø o con un par de llaves vacías { }.

El símbolo del conjunto vacío, ∅, se lee como "conjunto vacío" o simplemente "vacío".

Un Ejemplo Práctico del Conjunto Vacío

El conjunto de los números naturales impares que son divisibles por dos es vacío, ya que ningún número impar puede ser divisible por dos.

Solo existe un conjunto vacío. El conjunto de números naturales impares divisibles por dos es un conjunto vacío. Del mismo modo, el conjunto de triángulos con cuatro lados también es un conjunto vacío. En ambos casos, aunque las condiciones de pertenencia sean distintas, estamos hablando del mismo conjunto vacío. $$ Ø = \{ \ \ \} $$

El concepto de conjunto vacío plantea preguntas interesantes sobre la existencia en matemáticas, ya que es un objeto que, aunque no contiene nada, sí existe.

Podríamos describirlo como la "nada" que, paradójicamente, es "algo" dentro del mundo matemático.

El Conjunto Vacío como Subconjunto Impropio

El conjunto vacío es un subconjunto impropio de cualquier conjunto.

Demostración

Para demostrarlo, utilizamos un argumento por contradicción.

Sea A un conjunto cualquiera. Supongamos, en busca de una contradicción, que el conjunto vacío no es un subconjunto de A.

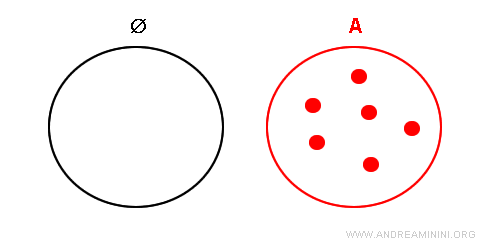
Esto implicaría que existe al menos un elemento en el conjunto vacío que no pertenece a A.

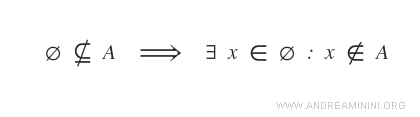
Sin embargo, esto es imposible, ya que el conjunto vacío no tiene elementos.

Una vez establecida esta contradicción, la suposición opuesta debe ser cierta: el conjunto vacío es, efectivamente, un subconjunto de A.

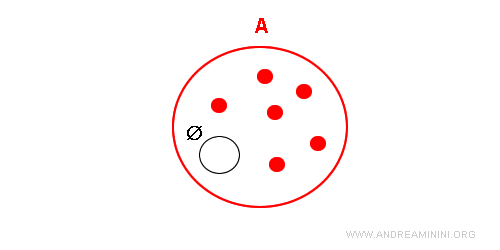
Por esta razón, el conjunto vacío se considera un subconjunto impropio de cualquier conjunto.

Otra Demostración. La unión de cualquier conjunto A con cualquiera de sus subconjuntos B⊆A siempre es igual al propio conjunto. $$ A \cup B = A $$ En particular, si tomamos B como el conjunto vacío, se cumple que: $$ A \cup Ø = A $$ Por lo tanto, el conjunto vacío es un subconjunto de A.

Propiedades Claves del Conjunto Vacío

• El conjunto vacío es único
  En matemáticas, existe un único conjunto vacío. No importa en qué contexto se mencione, siempre es el mismo objeto matemático.

  Esta unicidad es crucial, ya que garantiza que todas las propiedades asociadas al conjunto vacío sean universales e independientes de su contexto o notación. Por eso, siempre nos referimos a él en singular: "el conjunto vacío" y no "los conjuntos vacíos".

• Es subconjunto de cualquier conjunto
  Se considera un subconjunto impropio de cualquier otro conjunto.

  Recordemos la definición de subconjunto: un conjunto \(A\) es subconjunto de otro conjunto \(B\) si cada elemento de \(A\) pertenece también a \(B\). Como el conjunto vacío, \(\emptyset\), no tiene elementos, esta condición se cumple automáticamente para cualquier conjunto \(B\).

• Elemento neutro en la unión
  La unión de un conjunto A con el conjunto vacío Ø es el propio conjunto A, ya que el conjunto vacío no añade elementos. $$ A \cup \emptyset = A $$

  Ejemplo. Si A = {a, b, c} y B = { } (el conjunto vacío), su unión es simplemente A. $$ A \cup B = \{ a,b,c \} \cup \{ \ \} = \{a,b,c \} = A $$ $$ B \cup A = \{ \ \} \cup \{ a,b,c \} = \{a,b,c \} = A $$

• Elemento absorbente en la intersección
  La intersección de cualquier conjunto A con el conjunto vacío Ø siempre es el conjunto vacío. $$ A \cap \emptyset = \emptyset $$

  Ejemplo. Si A = {a, b, c} y B = { }, su intersección es el conjunto vacío. $$ A \cap B = \{ a,b,c \} \cap \{ \ \} = \emptyset $$ $$ B \cap A = \{ \ \} \cap \{ a,b,c \} = \emptyset $$

• Complemento
  El complemento del conjunto vacío en un conjunto universal \( U \) es el propio conjunto \( U \).
  

  $$ U \setminus ∅ = U $$

• Producto cartesiano
  El producto cartesiano de cualquier conjunto A con el conjunto vacío ∅ siempre es el conjunto vacío. $$ A \times ∅ = ∅ $$ $$ ∅ \times A = ∅ $$
• Conjunto potencia
  El conjunto potencia del conjunto vacío solo contiene al propio conjunto vacío. $$ P(∅) = \{\emptyset \} $$
• El conjunto vacío es abierto y cerrado en topología
  En cualquier espacio topológico, el conjunto vacío se considera simultáneamente abierto y cerrado.
• ¿El conjunto vacío es un subconjunto propio o impropio?
  En algunos textos matemáticos, el conjunto vacío (∅) se describe como un subconjunto impropio, mientras que en otros se le considera propio. Esta diferencia se debe a la definición específica de "subconjunto propio" utilizada en cada contexto.

Y así sucesivamente.