Conjunto parcialmente ordenado
Un conjunto provisto de un orden parcial se denomina conjunto parcialmente ordenado, o simplemente poset. Se representa como (A, ≤).
¿Qué se entiende por orden parcial?
Dado un conjunto A, un orden parcial es una relación
$$ ≤:A \times A \rightarrow \{ \text{verdadero}, \text{falso} \}. $$
En otras palabras, para cualquier par (x, y) en A, podemos determinar si se cumple o no la relación de orden ≤.
Un ejemplo concreto
Consideremos un conjunto finito A con siete elementos:
$$ A = \{ a, b, c, d, e, f \} $$
Definimos una relación ≤ sobre el producto cartesiano A × A:
$$ ≤ = \{ (a,c), (a,e), (b,d), (b,f), (c,g), (d,g), (e,g), (f,g) \} $$
El par (A, ≤) define un poset.
Nota. La relación no está definida para todos los pares de elementos del conjunto. Por ejemplo, no existe relación entre (a, b), (a, d), etc.
Las relaciones en el poset (A, ≤) pueden visualizarse mediante el siguiente grafo:
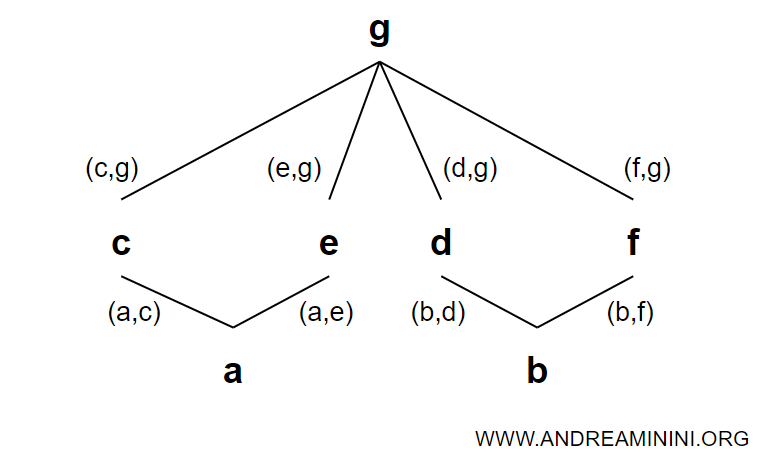
Cada flecha indica una relación de orden entre los elementos que conecta.
Otros ejemplos de posets
- Los números naturales
El conjunto \( (\mathbb{N}, \leq) \) de los números naturales, con el orden usual “menor o igual”, constituye un poset. Esta relación es reflexiva, antisimétrica y transitiva.Por ejemplo, dados dos elementos cualesquiera en \( \mathbb{N} = \{0, 1, 2, 3, \dots\} \), siempre es posible determinar cuál de ellos es menor o igual que el otro.
- El conjunto potencia ordenado por inclusión
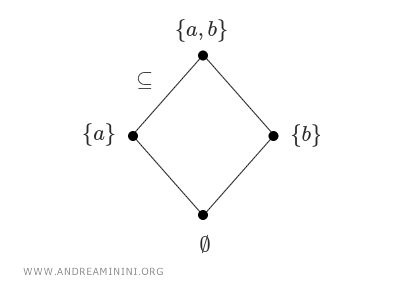
Si \( S \) es un conjunto, su conjunto potencia \( \mathcal{P}(S) \) - el conjunto de todos sus subconjuntos - forma un poset bajo la relación de inclusión (\(\subseteq\)). Aquí, el orden está determinado por la inclusión de conjuntos, no por valores numéricos.
Por ejemplo, si \( S = \{a, b\} \), entonces \( \mathcal{P}(S) = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} \). El conjunto vacío Ø está contenido en todos los demás, y tanto {a} como {b} están contenidos en {a, b}; sin embargo, {a, b} no está contenido ni en {a} ni en {b}. $$ \emptyset \subseteq \{ a \} \\ \{ a \} \subseteq \{a, b\} \\ \{ b \} \subseteq \{a, b\} \\ \vdots $$ Estas relaciones de inclusión pueden representarse mediante un diagrama de retículo, donde cada nodo representa un subconjunto y las aristas indican inclusión de abajo hacia arriba.
- La divisibilidad en los enteros
Otro ejemplo clásico de poset es el conjunto de los enteros \( \mathbb{Z} \), ordenado por la relación de divisibilidad. Decimos que \( x \mid y \) si x divide a y, lo cual define un orden parcial en ciertos subconjuntos de enteros.
Por ejemplo, 4 divide a 8 (4 | 8), por lo tanto la relación se cumple; pero 6 no divide a 8, así que 6 | 8 es falso. Consideremos el conjunto S = {2, 4, 6, 8, 12, 24} bajo esta relación. El diagrama de Hasse correspondiente representa cada número como un nodo, y las aristas (o cadenas de ellas) conectan divisores con sus múltiplos, de abajo hacia arriba.
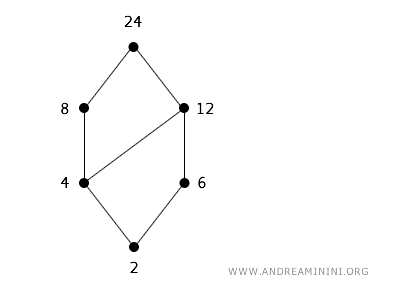
En este caso, 2 divide a todos los demás: 4, 6, 8, 12 y 24. No ocurre lo mismo en sentido inverso: por ejemplo, 6 divide a 12 y 24, pero no a 2, 4 ni 8.
Propiedades fundamentales de un poset
Un poset es un par (S, ≤) en el que S es un conjunto y ≤ una relación binaria que satisface las siguientes propiedades:
- Reflexividad: Todo elemento se relaciona consigo mismo: $$ \forall x \in S,\ x \le x $$
- Antisimetría: Si dos elementos se relacionan mutuamente, deben ser iguales: $$ \forall x, y \in S,\ (x \le y \land y \le x) \Rightarrow x = y $$
- Transitividad: Si x ≤ y e y ≤ z, entonces x ≤ z: $$ \forall x, y, z \in S,\ (x \le y \land y \le z) \Rightarrow x \le z $$
En síntesis, un poset es un conjunto con una relación reflexiva, antisimétrica y transitiva, pero no necesariamente total. Es decir, no todos los elementos del conjunto tienen que ser comparables entre sí.
Los posets son una noción central en la teoría de retículos y tienen aplicaciones en disciplinas como el álgebra conmutativa (por ejemplo, en el conjunto de ideales de un anillo) y la topología algebraica.
Ínfimo y supremo
Dado un poset (A, ≤) y un subconjunto B de A:
- El ínfimo de B, denotado inf(B), es el mayor elemento de A que es menor o igual que todos los elementos de B.
- El supremo de B, denotado sup(B), es el menor elemento de A que es mayor o igual que todos los elementos de B.
Ejemplo
El subconjunto B tiene ínfimo igual a 3 y supremo igual a 4.
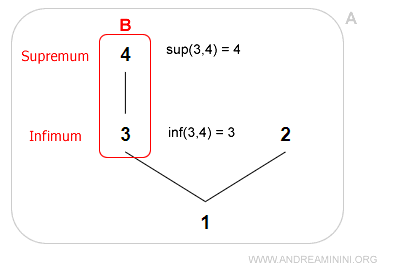
Nota. Un subconjunto no siempre posee un ínfimo o un supremo, pero si existen, son únicos.
Cotas inferior y superior
Sea (A, ≤) un poset y B un subconjunto de A:
- Un elemento \( k \in A \) es una cota inferior de B si \( k \le b \) para todo \( b \in B \).
Ejemplo. Si A = {1, 2, 3, 4, 5, 6} y B = {3, 4}, entonces las cotas inferiores de B son {1, 2, 3}.
- Un elemento \( k \in A \) es una cota superior de B si \( k \ge b \) para todo \( b \in B \).
Ejemplo. Con los mismos conjuntos A y B, las cotas superiores de B son {4, 5, 6}.
Elementos máximos y mínimos
En un poset (A, ≤):
- Un elemento mínimo es aquel que no está precedido por ningún otro elemento del conjunto A.
Ejemplo. En A = {1, 2, 3, 4, 5, 6}, el elemento mínimo es 1.
- Un elemento máximo es aquel que no está seguido por ningún otro elemento de A.
Ejemplo. En el mismo conjunto, el elemento máximo es 6.
Un poset puede tener múltiples elementos máximos o mínimos.
Ejemplo
El siguiente diagrama muestra tres elementos máximos y uno mínimo.
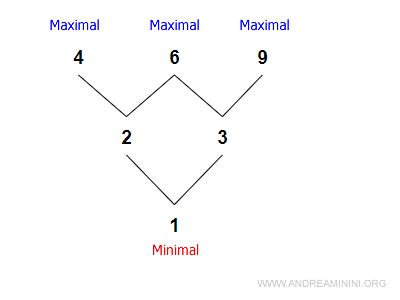
La relación de orden es la siguiente:
$$ ≤ = \{ (1,2), (1,3), (2,4), (2,6), (3,6), (3,9) \} $$
De ello se deduce que:
- 4, 6 y 9 no tienen sucesores en el conjunto: son elementos máximos.
- 1 no tiene predecesores: es el elemento mínimo.
Nota. En los posets infinitos no siempre existen elementos máximos o mínimos. En cambio, todo poset finito tiene al menos uno de cada tipo.
Máximo y mínimo
En un poset (A, ≤):
- El mínimo es el único elemento que es menor o igual que todos los demás elementos de A.
- El máximo es el único elemento que es mayor o igual que todos los demás elementos de A.
No todos los posets admiten un mínimo o un máximo.
Ejemplo
En el siguiente caso, 1 es el mínimo, pero no hay un máximo.
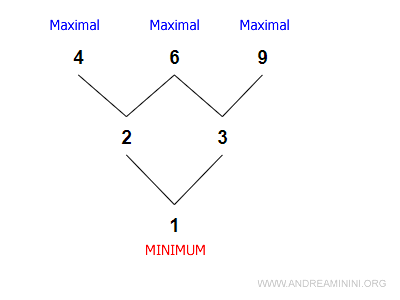
La relación de orden es:
$$ ≤ = \{ (1,2), (1,3), (2,4), (2,6), (3,6), (3,9) \} $$
Podemos comprobar que 1 es el mínimo, ya que:
$$ 1 \leq 2 \\ 1 \leq 3 \\ 1 \leq 4 \\ 1 \leq 6 \\ 1 \leq 9 $$
Sin embargo, no podemos concluir que 9 sea el máximo, ya que desconocemos si se cumplen las relaciones (2,9), (4,9) y (6,9):
$$ 1 \leq 9 \\ 3 \leq 9 \\ 2 \; ? \; 9 \\ 4 \; ? \; 9 \\ 6 \; ? \; 9 $$
Lo mismo ocurre con los demás candidatos a máximo:
4 no puede serlo, porque no sabemos si (4,9), (4,6) o (4,3) se verifican:
$$ 1 \leq 4 \\ 2 \leq 4 \\ 4 \; ? \; 3 \\ 4 \; ? \; 6 \\ 4 \; ? \; 9 $$
6 tampoco es el máximo, pues desconocemos si (6,4) o (6,9) se cumplen:
$$ 1 \leq 6 \\ 2 \leq 6 \\ 3 \leq 6 \\ 4 \; ? \; 6 \\ 9 \; ? \; 6 $$
Y así sucesivamente.