Teoría de Conjuntos
La teoría de conjuntos se basa en el uso del concepto de conjunto dentro del lenguaje lógico-matemático.
Definición de Conjunto
Un conjunto es una colección de objetos, conocidos como elementos o miembros, que comparten una propiedad específica. También se le puede llamar clase, conjunto o familia.
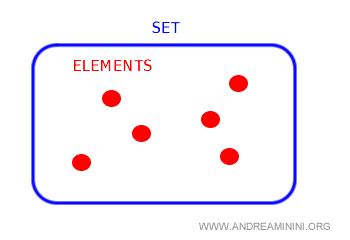
Este concepto es fundamental porque no puede definirse a partir de otros conceptos.
En un conjunto, el orden de los elementos no tiene importancia.
Definición de Conjunto en Matemáticas
En matemáticas, un conjunto es un grupo de objetos si existe un criterio objetivo que determina si cualquier objeto pertenece o no a dicho grupo.
Cuando se habla de un conjunto matemático, nos referimos a un conjunto específico en el que todos los objetos cumplen con un criterio objetivo de pertenencia.
En cambio, los conjuntos definidos por criterios subjetivos no se consideran conjuntos matemáticos.
De ahora en adelante, al mencionar "conjunto", me referiré a conjuntos matemáticos.
Ejemplo. El conjunto de números primos es un conjunto matemático, ya que el criterio de pertenencia es objetivo. Incluye todos los números naturales divisibles únicamente por 1 y por sí mismos. $$ I = \{ 2 , 3, 5, 7, 11, ... \} $$ Por el contrario, el conjunto de las mejores canciones no es un conjunto matemático porque el criterio de pertenencia es subjetivo y varía según la persona.
Representación de Conjuntos
En el lenguaje lógico-matemático, los conjuntos se representan con letras mayúsculas (A, B, C, D, ...).
Los elementos de un conjunto, en cambio, se representan con letras minúsculas (a, b, c, d, ...).
Símbolos de Pertenencia y No Pertenencia
El símbolo para indicar pertenencia a un conjunto es ∈.
Se lee como "el elemento x pertenece al conjunto A".
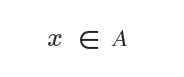
El símbolo para indicar que un elemento no pertenece a un conjunto es ∉.
Se lee como "el elemento x NO pertenece al conjunto A".
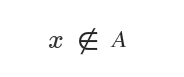
Ejemplo. Consideremos el conjunto B de números pares del 1 al 9. $$ B = \{ \ 2 \ , \ 4 \ , \ 6 \ , \ 8 \ \} $$ Para indicar que el número 2 pertenece al conjunto B, se escribe $$ 2 \in B $$ Para indicar que el número 3 NO pertenece al conjunto B, se escribe $$ 3 \notin B $$
Representación Gráfica
Para representar un conjunto gráficamente, se utilizan los diagramas de Euler-Venn, también conocidos como círculos de Euler.
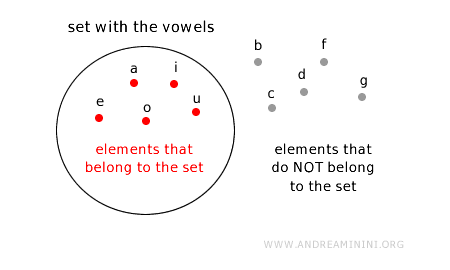
Cada conjunto se representa mediante un círculo, un óvalo o un polígono cerrado.
Los elementos que pertenecen al conjunto se colocan dentro del círculo.
Los elementos que no pertenecen al conjunto se sitúan fuera del círculo.
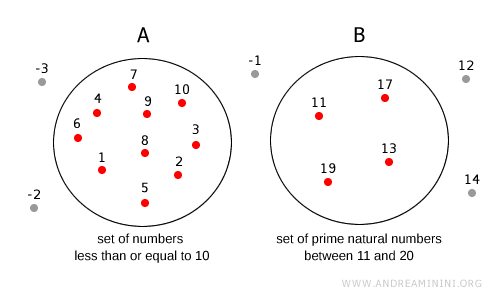
Nota. En el conjunto A se encuentran los números naturales hasta el 10. Todos los números fuera del círculo A no pertenecen al conjunto A. En el conjunto B, por otro lado, están los números primos entre 11 y 20. De igual manera, todos los números fuera del círculo B no pertenecen al conjunto B. Los números fuera de ambos círculos (-1, -2, -3, 12, 14, ...) no pertenecen ni al conjunto A ni al conjunto B.
Si un elemento pertenece a ambos conjuntos, debe estar dentro de ambos círculos.
Por ejemplo, si el conjunto B fuera el conjunto de números primos entre 1 y 20, tendría que representar los conjuntos A y B intersectándose.

En este caso, los elementos comunes a ambos conjuntos A⋂B={1, 2, 3, 5, 7} están incluidos en ambos, A y B.
Nota. Los diagramas de Euler-Venn llevan el nombre del matemático suizo Leonhard Euler y del matemático inglés John Venn, quienes fueron los primeros en utilizarlos para representar conjuntos.
Representación Tabular o Enumerativa
Un conjunto sencillo también puede representarse de manera tabular.
En la representación tabular, los elementos del conjunto se escriben entre llaves y se separan por comas.
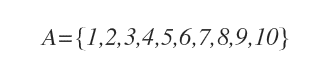
A esta representación también se la conoce como notación enumerativa.
No es necesario listar los elementos en un orden específico. El orden de los elementos no importa.
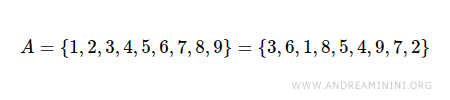
Cualquier elemento repetido dentro del conjunto debe aparecer solo una vez en la notación enumerativa.
Por lo tanto, no debe haber elementos repetidos entre las llaves.
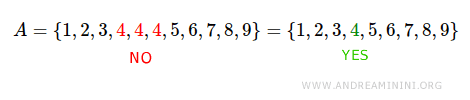
La representación tabular es útil cuando el conjunto es finito y tiene pocos elementos.
Resulta engorrosa cuando el conjunto contiene muchos elementos.
Nota. A veces se usan puntos suspensivos ... cuando la regla de pertenencia al conjunto es lo suficientemente clara y los elementos no listados explícitamente se sobreentienden. Por ejemplo, A={1,2,...,10} significa los números naturales del 1 al 10. $$ A = \{ \ 1,2, \ ... \ ,10 \ \} $$ En la representación tabular, los puntos suspensivos ... también indican un conjunto con elementos infinitos. Por ejemplo, A={1,2,3,...} significa todos los números naturales a partir del 1. $$ A=\{ \ 1,2,3 \ ... \ \} $$
Notación de Comprensión
Un conjunto también puede representarse mediante la notación de comprensión, basada en la regla o propiedad de pertenencia al conjunto.
Esta notación es útil cuando el conjunto tiene muchos o infinitos elementos.
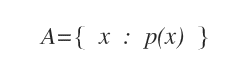
Dentro de las llaves, la regla de pertenencia al conjunto, también conocida como la propiedad característica, se indica mediante el lenguaje formal de la lógica matemática.
Ejemplo. En notación de comprensión, los números naturales del 1 al 10 se representan como A={x∈N:0<x≤10}.
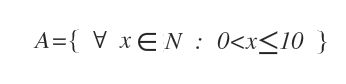
Donde x es una variable que indica cualquier número natural x∈N. El símbolo ∀ se lee "para todo". Los dos puntos : se leen "tal que". A veces, también se usa el símbolo | para significar "tal que". $$ A = \{ \ \forall \ x \in N \ | \ 0<x \le 10 \} $$ Por lo tanto, la notación anterior se lee de la siguiente manera: "A es el conjunto de números naturales x tales que x es un número entre 0 y 10".
Ventajas y Desventajas de las Notaciones
La notación de comprensión puede usarse para representar cualquier tipo de conjunto, finito o infinito, siempre que los elementos puedan identificarse mediante uno o varios criterios.
La notación enumerativa, en cambio, solo puede utilizarse si:
- el conjunto es finito y tiene pocos elementos
- el conjunto es finito/infinito y puede representarse indicando explícitamente solo algunos elementos y dejando implícitos los demás.
Por último, la notación gráfica es especialmente útil para explicar o comunicar visualmente conceptos que, de otra manera, serían difíciles de comprender con la notación lógico-matemática.
Conjuntos Finitos e Infinitos
Un conjunto puede ser finito o infinito.
- Un conjunto finito consta de un número finito n de elementos.
Ejemplo. El conjunto de libros en una mochila es un conjunto finito. Otro ejemplo de conjunto finito es el conjunto de granos de arena en un recipiente.
- Un conjunto infinito consta de un número infinito de elementos.
Ejemplo. El conjunto de números naturales es un conjunto infinito, ya que cada número natural (n) tiene un sucesor (n+1). No existe un número natural que sea mayor que todos los demás.
Conjuntos Numéricos
Los conjuntos numéricos son conjuntos compuestos por números
Por convención, en matemáticas, los conjuntos numéricos se escriben con letras mayúsculas específicas.
- N representa el conjunto de números naturales
- Z representa el conjunto de números enteros
- Q representa el conjunto de números racionales
- I representa el conjunto de números irracionales
- R representa el conjunto de números reales
- C representa el conjunto de números complejos
El Conjunto Vacío
El conjunto vacío es un conjunto sin elementos. Se representa con el símbolo Ø. $$ Ø = \{ \ \ \} $$
A veces, el conjunto vacío también se indica con dos llaves sin elementos dentro.
Es un conjunto especial porque el conjunto vacío es un subconjunto de cualquier otro conjunto.
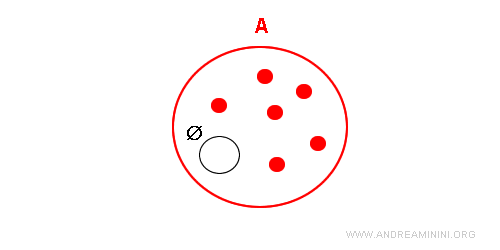
Solo existe un conjunto vacío. Por ejemplo, el conjunto de números naturales impares divisibles por dos es un conjunto vacío, ya que ningún número natural impar es divisible por dos. De la misma manera, el conjunto de cuadrados con tres lados es un conjunto vacío, ya que cada cuadrado tiene cuatro lados. En ambos casos, es el mismo conjunto vacío, aunque los criterios de pertenencia difieren.
Y así sucesivamente.