Relaciones Matemáticas
¿Qué es una relación?
Una relación es una regla que asocia ciertos elementos del conjunto A con uno o más elementos del conjunto B. $$ aRb $$ Donde a∈A y b∈B, y el elemento b se conoce como la imagen de a.
Es importante destacar que he dicho "ciertos" elementos porque la regla no tiene por qué aplicarse a todos los elementos de A.
De la misma manera, tampoco es necesario que involucre a todos los elementos de B.
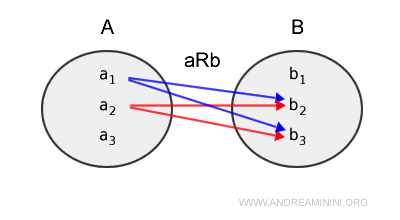
Además, un mismo elemento de A puede estar relacionado con varios elementos de B.
El diagrama de Venn anterior también se puede representar de la siguiente forma:

Así pues, una relación no es más que un subconjunto del producto cartesiano AxB entre ambos conjuntos.
$$ R \subseteq AxB $$
Nota. Cuando el conjunto A coincide con el conjunto B, es decir, A=B, se dice que la relación matemática está definida en A.
Un Ejemplo Práctico
Supongamos que tenemos dos conjuntos, A y B:
$$ A = \{ 2, 4, 6, 8 \} \\ B = \{ 1, 3, 5 \} $$
El producto cartesiano AxB está formado por todos los pares ordenados (a,b) donde a∈A y b∈B.
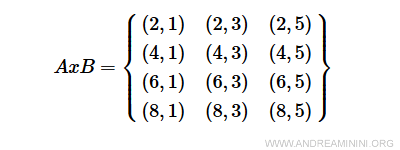
Ahora definimos una relación R que asocia los pares (a,b) tales que se cumpla la condición a+2b<10.
Por ejemplo, el par (a,b)=(2,1) pertenece a R porque 2+2·1=4<10.
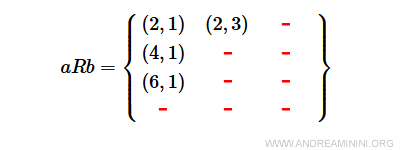
Nota. Todo par (a,b) pertenece al producto cartesiano AxB, por lo que una relación es, en realidad, un subconjunto de dicho producto.
La relación R selecciona solo un subconjunto de AxB.
En este caso, los pares (2,1), (2,3), (4,1) y (6,1) cumplen la condición impuesta por R, mientras que el resto no.
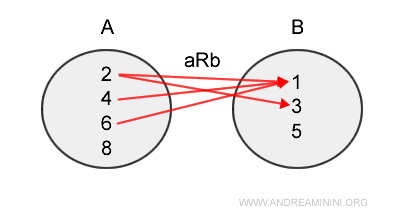
Por lo tanto, el subconjunto aRb está compuesto por cuatro elementos:
$$ aRb = \{ (2,1), (2,3), (4,1) , (6,1) \} \subset AxB $$
Nota. Existen infinitas relaciones posibles entre los conjuntos A y B, y esta es solo una de muchas. Por ejemplo, si definimos otra relación R' con la condición 2a+b<10, el subconjunto aR'b será completamente distinto al anterior: $$ aR'b = \begin{Bmatrix} (2,1) & ( 2,3 ) & (2,5) \\ (4,1) & - & - \\ - & - & - \\ - & - & - \end{Bmatrix} $$
Ejemplo
Volvamos a los conjuntos A y B y a la relación R: a+2b<10.
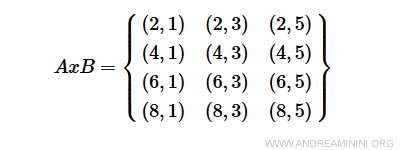
Los elementos de A que satisfacen la relación son 2, 4 y 6.
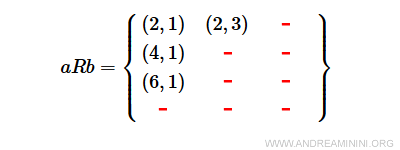
Así, el dominio de R está formado por los elementos 2, 4 y 6 del conjunto A, mientras que el codominio de R lo componen los elementos 1 y 3 del conjunto B.
$$ \text{dom(R)} = \{2, 4, 6 \} $$
$$ \text{codom(R)} = \{1,3 \} $$
Nota. En algunos textos matemáticos, el dominio se considera simplemente el conjunto A, sin distinguir entre los elementos que tienen imagen en B a través de R y los que no la tienen. En este caso, el dominio incluiría todos los elementos de A: $$ \text{dom(R)} = \{2, 4, 6, 8 \} $$ El subconjunto de A donde realmente está definida la relación R recibe el nombre de conjunto de definición o campo de existencia de R: $$ \text{conjunto de definición} = \{2, 4, 6 \} $$
Representación de una Relación
Existen diversas formas de representar una relación binaria entre dos conjuntos:
- Representación por enumeración
Se enumeran los pares ordenados (a,b) que cumplen la relación. $$ aRb = \{ (2,1), (2,3), (4,1), (6,1) \} $$ - Diagrama de flechas
Es la representación visual clásica de una relación entre dos conjuntos, donde se trazan flechas que conectan elementos de A con elementos de B.
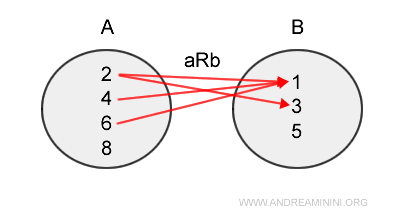
- Matriz de la relación (o tabla de doble entrada)
También se puede representar la relación mediante una matriz de relación, organizando los elementos de A en filas y los de B en columnas. En cada celda, se coloca:- 1 si el par (a,b) pertenece a la relación R.
- 0 si el par (a,b) no pertenece a R.
Ejemplo práctico. El producto cartesiano AxB es:
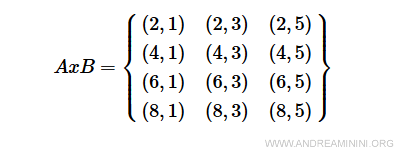
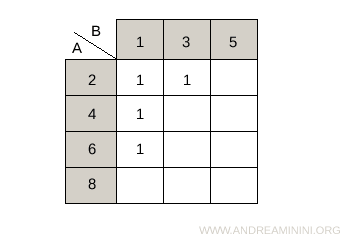
La relación aRb definida por la condición a+2b<10 se representa con la siguiente matriz de relación, donde los elementos de A se ubican en las filas y los de B en las columnas. $$ aRb = \begin{Bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{Bmatrix} $$ Para una representación más intuitiva, también se puede usar una tabla de doble entrada.
- Representación cartesiana
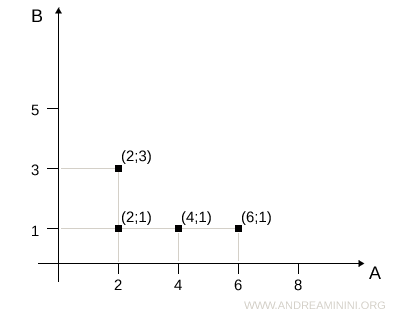
En un diagrama cartesiano, los elementos de A (dominio) se representan en el eje horizontal, mientras que los de B (codominio o imagen) se colocan en el eje vertical. Los puntos en el plano corresponden a los pares ordenados (a,b) que cumplen la relación.
La Relación Inversa
Dada una relación \( b=R(a) \), su relación inversa \( a=R^{-1}(b) \) asocia los elementos de B con los elementos de A.
La relación inversa \( bR^{-1}a \) existe si y solo si la relación \( aRb \) existe.
$$ bR^{-1}a \Leftrightarrow aRb $$
Por lo tanto, el dominio de la relación inversa \( R^{-1} \) coincide con el codominio de la relación \( R \):
$$ dom \ R^{-1} = codom \ R $$
Asimismo, el codominio de \( R^{-1} \) coincide con el dominio de \( R \):
$$ codom \ R^{-1} = dom \ R $$
Ejemplo práctico
Tomemos nuevamente los conjuntos A y B con la relación R: a+2b<10
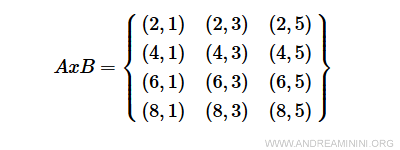
Los elementos de A que cumplen la relación son 2, 4 y 6.
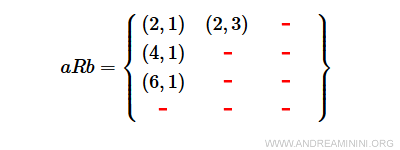
La relación de A a B es:
$$ aRb = \{ (2,1), (2,3), (4,1) , (6,1) \} \subset AxB $$
La relación inversa de B a A es:
$$ bR^{-1}a = \{ (1,2), (3,2), (1,4) , (1,6) \} \subset BxA $$
La relación inversa tiene la dirección opuesta a la original.
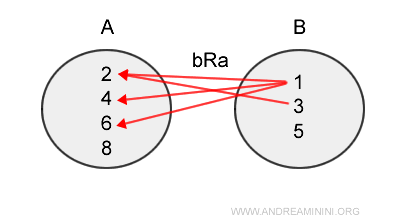
Nota. En \( aRb \), los pares son (a,b). En la relación inversa, los pares se intercambian, es decir, (b,a).
Tipos de Relaciones
Las relaciones pueden clasificarse en los siguientes tipos:
- Funciones (o aplicaciones)
- Relaciones binarias
Una relación binaria entre dos conjuntos A y B es un subconjunto del producto cartesiano AxB. Se expresa como: $$ aRb \ \ a \in A, \ \ b \in B $$ Se llama binaria porque asocia elementos de dos conjuntos, generando pares ordenados (a,b): $$ (a,b) \in aRb $$ - Relaciones de orden
Cumplen las propiedades de reflexividad, antisimetricidad y transitividad. - Relaciones de equivalencia
Cumplen las propiedades de reflexividad, simetría y transitividad. - Relaciones de compatibilidad
Son reflexivas y simétricas, pero no transitivas.
Cada tipo de relación tiene propiedades que la caracterizan.
- Una relación es reflexiva si $$\forall a \in A \Rightarrow (a,a) \in R $$
- Una relación es simétrica si $$ \forall (a,b) \in R \Rightarrow (b,a) \in R $$
- Una relación es antisimétrica si $$ \forall (a,b) \in R \ \text{y} \ (b,a) \in R \Rightarrow a=b $$
- Una relación es transitiva si $$ \forall (a,b) \in R, \ (b,c) \in R \Rightarrow (a,c) \in R $$
Las propiedades de reflexividad, simetría y transitividad son independientes entre sí, por lo que algunas relaciones pueden cumplir unas y no otras.