Relaciones Transitivas
¿Qué es una relación transitiva?
Una relación se dice transitiva cuando, dados tres elementos cualesquiera a, b y c de un conjunto I, si a está relacionado con b y b está relacionado con c, entonces a también debe estar relacionado con c. $$ \forall \ a,b,c \in I \ | \ aRb \ , \ bRc \ \Rightarrow aRc $$ Esta propiedad puede visualizarse de forma gráfica del siguiente modo:
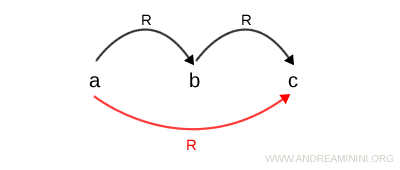
Se denominan transitivas porque cumplen con la propiedad transitiva.
Por ejemplo, si A es hermano de B y B es hermano de C, entonces A también es hermano de C.
Las relaciones transitivas forman parte del conjunto más amplio de relaciones definidas sobre un conjunto.
Nota: No todas las relaciones son transitivas. Por ejemplo, si A es madre de B y B es madre de C, eso no implica que A sea madre de C, por lo tanto esta relación no es transitiva.
Un ejemplo práctico
Consideremos el conjunto I:
$$ I = \{ 2 , 4, 6, 8, 10 \} $$
La relación R vincula pares de números pares.
Por ejemplo, 2 y 4 están relacionados porque ambos son números pares:
$$ 2R4 $$
Asimismo, 4 y 6 también están relacionados por la misma razón:
$$ 4R6 $$
Aplicando la propiedad transitiva, 2 y 6 deben estar relacionados: si 2 está relacionado con 4 y 4 lo está con 6, entonces 2 también lo está con 6:
$$ 2R6 $$
En este caso, la propiedad transitiva se cumple para todas las combinaciones posibles de elementos del conjunto I = {2, 4, 6, 8, 10}.
Por lo tanto, la relación R es transitiva en el conjunto I.
Nota: Las relaciones transitivas suelen representarse mediante gráficas. En estos esquemas, la propiedad transitiva se detecta fácilmente observando las conexiones entre los nodos (los elementos del conjunto). Por ejemplo, si existe una flecha de 2 a 4 y otra de 4 a 6, también debe haber una flecha directa de 2 a 6.
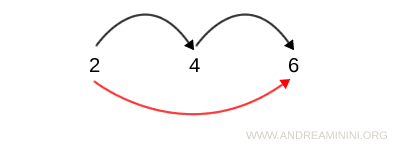
En cambio, las tablas de doble entrada y los diagramas cartesianos no permiten identificar esta propiedad con la misma claridad.
Más ejemplos
- La relación "x es perpendicular a y" NO es transitiva. Si la recta x forma un ángulo de 90° con la recta y, y esta a su vez forma un ángulo de 90° con la recta z, entonces x y z forman un ángulo de 180° (una recta) o de 0° (coinciden). En ambos casos, x y z no son perpendiculares.