Relaciones Definidas en un Conjunto

Se dice que una relación está definida en un conjunto cuando vincula elementos de un conjunto A con otros elementos del mismo conjunto A.

En este contexto, el dominio y el codominio coinciden.

Este tipo de relación constituye un subconjunto del producto cartesiano A × A.

Un Ejemplo Práctico

Tomemos como referencia el conjunto finito A:

$$ A = \{ 2,3,4,5,6,7,8,9 \} $$

El producto cartesiano de A consigo mismo, es decir A × A, se representa así:

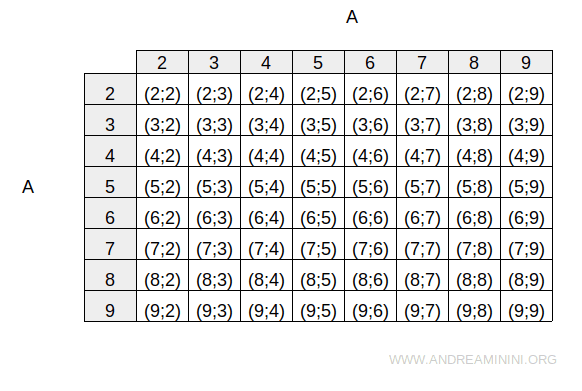
Definimos una relación R sobre A que asocia cada elemento con sus múltiplos:

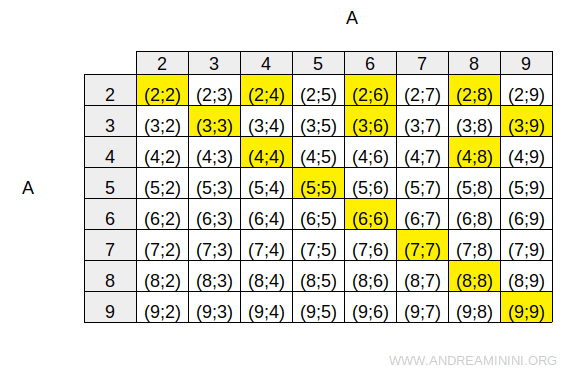
$$ R = \{ (2;2) , (2;4),(2;6),(2;8),(3;3),(3;6),(3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4) , (4;8),(5;5),(6;6),(7;7),(8;8),(9;9) \} $$

Esta relación es, por tanto, un subconjunto del producto cartesiano A × A.

A continuación, observamos cómo se representa la relación en una tabla de doble entrada:

El diagrama de flechas (también llamado diagrama de mapeo) de esta relación es el siguiente:

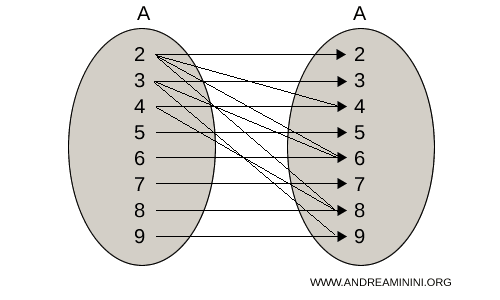
En este caso, el conjunto A actúa tanto como dominio como codominio.

Veamos ahora el correspondiente diagrama cartesiano de la relación:

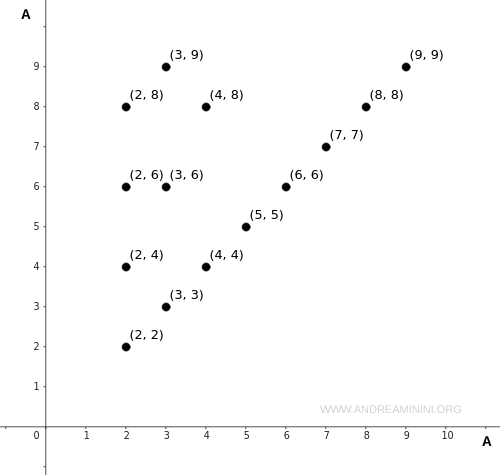
Como puede verse, el conjunto A se dispone en ambos ejes: el horizontal (eje x) y el vertical (eje y).

Nota. Las relaciones definidas sobre un conjunto pueden representarse de forma más intuitiva mediante un grafo. Basta con representar cada elemento de A como un nodo, sin necesidad de encerrarlo en un contorno, y trazar arcos dirigidos entre los elementos relacionados. Cuando un elemento está relacionado consigo mismo - como en el caso de (2;2) - se genera un tipo especial de arco llamado bucle. En general, las representaciones gráficas son más claras, compactas y eficaces desde el punto de vista visual.

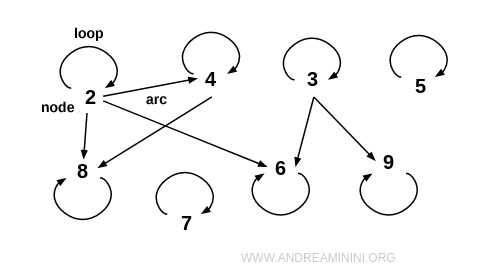
Tipos de Relaciones Definidas en un Conjunto

Entre las relaciones que se pueden definir en un conjunto, destacan varias categorías fundamentales:

• Relación Reflexiva
  Una relación R definida en un conjunto A es reflexiva si todo elemento a ∈ A está relacionado consigo mismo. $$ \forall \ a \in A \Rightarrow \ aRa $$
• Relación Irreflexiva
  La relación R es irreflexiva si ningún elemento a ∈ A está relacionado consigo mismo. $$ \forall \ a \ \in A \ \Rightarrow a \require{cancel} \cancel{R} a $$
• Relación Simétrica
  R es simétrica si, para todos a y b en A, el hecho de que a esté relacionado con b implica que b también lo está con a. $$ aRb \ \Leftrightarrow \ bRa $$
• Relación Asimétrica
  R es asimétrica si, para todos a y b en A, cuando a está relacionado con b, entonces b no está relacionado con a. $$ aRb \Rightarrow b \require{cancel} \cancel{R} a $$
• Relación Antisimétrica
  R es antisimétrica si, para todos los elementos a y b de A tales que a ≠ b, si a está relacionado con b, entonces b no está relacionado con a. $$ aRb , \ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$

  ¿Cuál es la diferencia entre asimétrica y antisimétrica? Una relación antisimétrica permite la reciprocidad solo si los elementos coinciden. Es decir, si a está relacionado con b y b con a, entonces necesariamente a = b. $$ aRb , \ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$ En cambio, una relación asimétrica prohíbe toda reciprocidad, incluso entre elementos iguales. $$ aRb \Rightarrow b \require{cancel} \cancel{R} a $$ En resumen, la asimetría descarta por completo las relaciones mutuas, mientras que la antisimetría las admite únicamente entre elementos idénticos.

• Relación Transitiva
  Una relación R definida en un conjunto A es transitiva si, siempre que a esté relacionado con b y b con c, entonces a también está relacionado con c. $$ aRb , \ bRc \Rightarrow aRc $$

Y así sucesivamente.