Relación Inversa

Dada una relación aRb definida sobre el producto cartesiano A×B, su relación inversa bR^-1a es el subconjunto de B×A que contiene todos los pares (b, a) tales que se cumple aRb.

Dicho de otro modo, si aRb es una relación que va del conjunto A al conjunto B, entonces la relación inversa bR^-1a establece una correspondencia desde B de regreso a A.

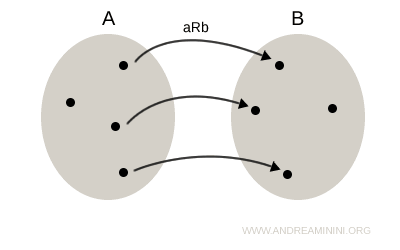
La relación inversa R^-1 se construye invirtiendo el orden de cada par (a, b), de manera que se obtiene (b, a).

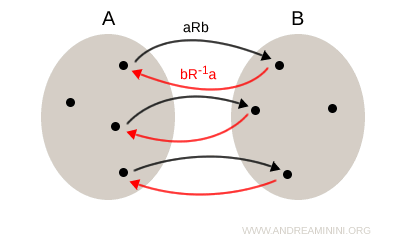
Visualmente, la relación inversa se representa invirtiendo el sentido de las flechas: por cada flecha aRb que va de A a B, aparece una flecha correspondiente bR^-1a que va de B a A.

En consecuencia, el dominio de la relación inversa coincide con el codominio de la relación original:

$$ \text{dominio} \ R^{-1} = \text{codominio} \ R $$

Y su codominio corresponde al dominio de la relación original:

$$ \text{codominio} \ R^{-1} = \text{dominio} \ R $$

Nota: La relación inversa bR^-1a se verifica si y solo si se verifica la relación original aRb. $$ bR^{-1}a \Leftrightarrow aRb $$

Un ejemplo práctico

Consideremos dos conjuntos finitos A y B:

$$ A = \{2,3,4,5,6 \} $$

$$ B = \{4,9,16,25,36 \} $$

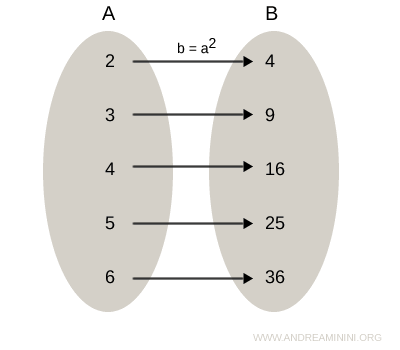
La relación R asocia a cada elemento de A su cuadrado en B:

$$ aRb \ : \ b = a^2 $$

Esta relación es un subconjunto del producto cartesiano A×B, y está formada por los siguientes pares ordenados (a, b):

$$ aRb = \{ (2,4), (3,9), (4,16), (5,25), (6,36) \} \subset A×B $$

A continuación se muestra el diagrama sagital que representa la relación aRb:

La relación inversa R^-1 vincula