Relaciones de Orden

Las relaciones de orden son relaciones matemáticas que cumplen tres propiedades fundamentales: reflexividad, antisimetría y transitividad.

• Reflexividad: $$ \forall \ a \in A \:\: a\rho a $$
• Antisimetría: $$ \forall \ a,b \in A \ , \ a\rho b , \ a \ne b \Rightarrow b \require{cancel} \cancel{\rho} a $$
• Transitividad: $$ \forall \ a,b,c \in A :\: [ a\rho b \land b\rho c ] \rightarrow a\rho c $$

Este tipo de relación también se denomina orden no estricto.

Existe un concepto relacionado, el de orden estricto, en el cual la propiedad de reflexividad se reemplaza por la de irreflexividad.

En general, una relación se considera de orden si es reflexiva (o irreflexiva), antisimétrica y transitiva.

Ejemplo práctico

Analicemos el conjunto de los números naturales:

$$ N = \{ 1, 2, 3, 4, ... \} $$

Queremos determinar si la relación R: "x es múltiplo de y" constituye una relación de orden.

Para ello, evaluamos si satisface las tres propiedades fundamentales:

• Reflexividad: Todo número es múltiplo de sí mismo (por ejemplo, x = 1·x).
• Antisimetría: Si x e y son distintos y x es múltiplo de y, entonces y no puede ser múltiplo de x.
• Transitividad: Si x es múltiplo de y y y es múltiplo de z, entonces x también es múltiplo de z.

Como se cumplen las tres condiciones, R es efectivamente una relación de orden.

Órdenes estrictos y no estrictos

Las relaciones de orden se clasifican en dos grandes categorías:

• Relaciones de orden no estricto
  Estas satisfacen reflexividad, antisimetría y transitividad.

  Ejemplo: La relación "x es múltiplo de y" es un orden no estricto. Es reflexiva (todo número es múltiplo de sí mismo, como 2·1=2 o 3·1=3), y además cumple antisimetría y transitividad.

• Relaciones de orden estricto
  Estas cumplen irreflexividad, antisimetría y transitividad.

  Ejemplo: La relación "x es más alto que y" es un orden estricto. Es irreflexiva (nadie puede ser más alto que sí mismo), y también presenta antisimetría y transitividad.

En síntesis, los órdenes estrictos son irreflexivos, mientras que los no estrictos son reflexivos.

Órdenes parciales y totales

Los órdenes, tanto estrictos como no estrictos, pueden subdividirse según el grado de comparabilidad que establecen sobre un conjunto. Una relación de orden puede ser total o parcial:

• Orden parcial

  Un orden parcial compara únicamente algunos pares de elementos, lo que implica que no todos los elementos del conjunto pueden ser comparados entre sí.

  Se define sobre un subconjunto del producto cartesiano. En este contexto, el conjunto recibe el nombre de conjunto parcialmente ordenado, ya que solo ciertos pares de elementos resultan comparables.

  Ejemplo: El conjunto potencia P(X), con X = {1, 2, 3}, contiene los siguientes subconjuntos: {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}. Bajo la relación de inclusión ⊆, se forma un orden parcial: por ejemplo, {1} ⊆ {1,2}, mientras que {3} no está incluido en {1,2}. Su estructura se representa así:
  

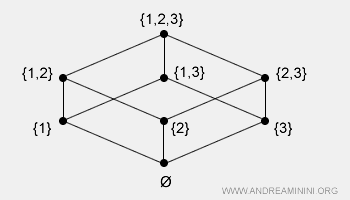
• Orden total

  Un orden total permite comparar cualquier par de elementos del conjunto: todos los elementos son comparables entre sí.

  Se aplica a todos los pares (a, b) del conjunto. En este caso, el conjunto se denomina totalmente ordenado o cadena, debido a su estructura lineal: cualquier par de elementos admite comparación.

  Ejemplo: El conjunto X = {1, 2, 3} puede ordenarse totalmente usando la relación ≤ (o ≥). En este caso, todos los pares de elementos son comparables: 1ρ2, 2ρ3, 1ρ3, etc. El diagrama asociado forma una cadena, ya que cada elemento se compara directamente con los demás.
  

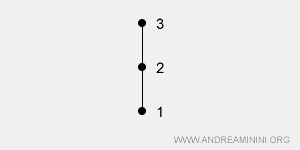
Visualización de relaciones de orden

Las relaciones de orden sobre un conjunto X pueden representarse gráficamente mediante diagramas de puntos conectados por líneas.

Cada punto representa un elemento del conjunto.

Un segmento une dos elementos cuando son directamente comparables según la relación, es decir, cuando no existe ningún elemento intermedio entre ellos.

Ejemplo: En la relación ≤, los elementos 1 y 3 son comparables. No obstante, dado que 2 se encuentra entre ambos, no se traza un enlace directo. En cambio, 1 y 2 sí se conectan, al igual que 2 y 3, ya que entre ellos no hay elementos intermedios.

Conjuntos ordenados isomorfos

Dos conjuntos ordenados se consideran isomorfos cuando comparten la misma estructura relacional entre sus elementos.

Por ejemplo, cualquier par de conjuntos totalmente ordenados con la misma cardinalidad serán siempre isomorfos.

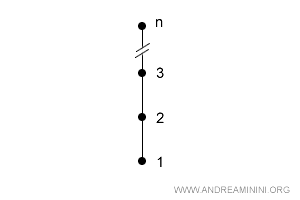
En definitiva, los conjuntos isomorfos presentan la misma estructura de relaciones, aunque sus elementos puedan ser distintos.

Y así sucesivamente.