Relaciones Reflexivas
¿Qué es una relación reflexiva?
Una relación definida sobre un conjunto A se denomina reflexiva si cada elemento de A está relacionado consigo mismo. $$ \forall \ a \in \ A \ , \ aRa $$
En otras palabras, una relación reflexiva establece un vínculo entre cada elemento del conjunto y él mismo.
Por ejemplo, la relación "X tiene la misma edad que Y" es reflexiva, ya que toda persona, naturalmente, tiene la misma edad que sí misma.
Las relaciones reflexivas forman parte del conjunto más amplio de relaciones definidas en un conjunto.
Un Ejemplo Concreto
Consideremos el conjunto A:
$$ A = \{ 2,3,4,5,6,7,8,9 \} $$
Definimos una relación R que asocia cada elemento de A con sus múltiplos, siempre que también pertenezcan al conjunto.
$$ R = \{ (2;2), (2;4), (2;6), (2;8), (3;3), (3;6), (3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4), (4;8), (5;5), (6;6), (7;7), (8;8), (9;9) \} $$
Esta relación constituye un subconjunto del producto cartesiano AxA, es decir, del conjunto de todos los pares ordenados formados por elementos de A.
Podemos representar esta relación mediante una tabla de doble entrada.
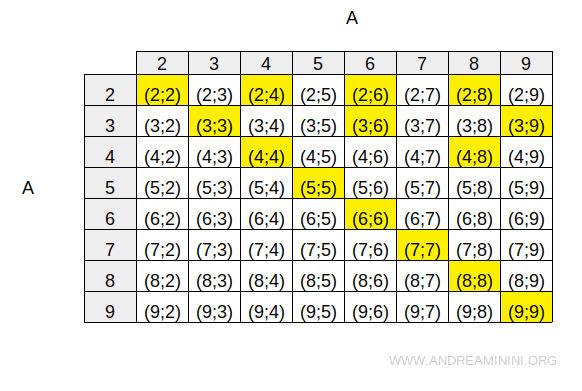
Las celdas en amarillo indican los pares del producto AxA que cumplen la relación R.
Observamos que cada elemento se relaciona consigo mismo.
La diagonal principal de la tabla contiene únicamente pares ordenados que pertenecen a la relación (y que aparecen resaltados en amarillo), como (2;2), (3;3), (4;4), y así sucesivamente.
Esto confirma que R es, efectivamente, una relación reflexiva.
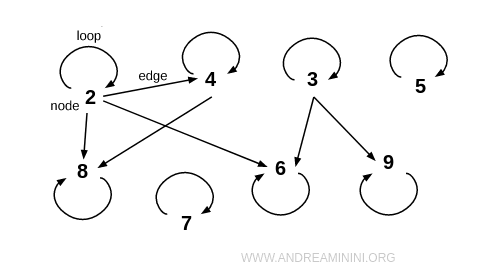
Nota. En una representación mediante grafo, una relación es reflexiva si cada nodo presenta un bucle, es decir, una arista que lo conecta consigo mismo. Esta característica visual permite identificar la reflexividad de forma inmediata.
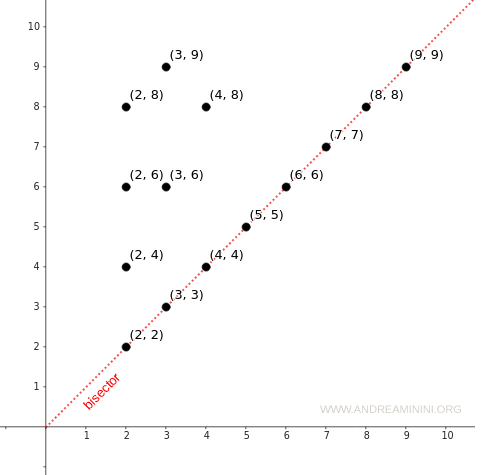
En un diagrama cartesiano, una relación es reflexiva si todos los elementos de A aparecen como pares ordenados sobre la diagonal (la bisectriz), según la relación R. También en este caso, la reflexividad puede detectarse de un solo vistazo.
Otros Ejemplos
- La relación "x es perpendicular a y" no es reflexiva, ya que ninguna recta puede formar un ángulo de 90° consigo misma.
Y así sucesivamente.