Relaciones Irreflexivas

¿Qué es una relación irreflexiva?

Una relación definida sobre un conjunto I se denomina irreflexiva (o también antirreflexiva) si ningún elemento del conjunto está relacionado consigo mismo. $$ \forall \ a \in I \ , \ a \require{cancel} \cancel{R} a $$

En una relación irreflexiva, absolutamente ningún elemento se encuentra vinculado consigo mismo.

Por ejemplo, la relación “A es la madre de B” es irreflexiva, ya que nadie puede ser su propia madre.

Las relaciones irreflexivas constituyen una subclase particular dentro de las relaciones definidas en un conjunto.

Un Ejemplo Práctico

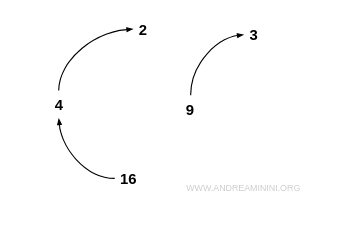
Consideremos el conjunto finito I:

$$ I = \{ 2,4,3,9,16 \} $$

Definimos una relación R que asocia cada elemento con su raíz cuadrada; es decir: "x es la raíz cuadrada de y".

$$ R = \{ (4;2), (16;4), (9;3) \} $$

Esta relación es irreflexiva porque ninguno de los elementos del conjunto I es raíz cuadrada de sí mismo.

Nota. Por ejemplo, 2 no es la raíz cuadrada de 2. $$ 2 \ne \sqrt{2} $$ Lo mismo ocurre con todos los demás elementos de I. En una representación mediante grafo, una relación irreflexiva se caracteriza por la ausencia total de bucles: ningún nodo se conecta consigo mismo.

Observaciones Adicionales

Algunas consideraciones importantes sobre las relaciones irreflexivas:

• Existen relaciones que no son ni reflexivas ni irreflexivas. Es decir, que una relación no sea irreflexiva no implica necesariamente que sea reflexiva, y viceversa.

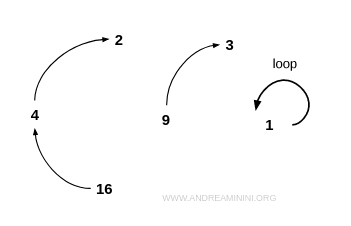
  Ejemplo. Consideremos el conjunto $$ I = \{1,2,3,4,9,16 \} $$ y la relación R definida como "x es la raíz cuadrada de y". Esta relación no es reflexiva, ya que no todos los elementos están relacionados consigo mismos - por ejemplo, 2 no es raíz cuadrada de 2. $$ 2 \ne \sqrt{2} $$ Pero tampoco es irreflexiva, pues contiene al menos un par reflexivo: por ejemplo, 1 es raíz cuadrada de 1. $$ 1 = \sqrt{1} $$ En el grafo que representa esta relación, el nodo 1 tiene un bucle. Esto indica que la relación no es irreflexiva. Sin embargo, como no todos los nodos presentan bucles, tampoco es reflexiva.
  

Y así sucesivamente.