Relaciones Antisimétricas

¿Qué es una relación antisimétrica?

Una relación definida sobre un conjunto X se denomina antisimétrica si, para cualquier par de elementos distintos, cuando a está relacionado con b, entonces b no está relacionado con a: $$ a R b \ ,\ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$

En otras palabras, en una relación antisimétrica ningún par de elementos distintos puede estar relacionado en ambos sentidos.

Por ejemplo, la relación “A es mayor o igual que B” es antisimétrica: si A ≥ B y A ≠ B, entonces no es posible que B ≥ A.

Esta propiedad permite la reciprocidad únicamente cuando los elementos son iguales.

Diferencias entre antisimetría y asimetría. Aunque puedan parecer similares a primera vista, las relaciones antisimétricas y asimétricas expresan conceptos distintos. En una relación antisimétrica, se permite reciprocidad solo entre elementos idénticos. En una relación asimétrica, toda reciprocidad está prohibida, incluso entre elementos iguales. Por ejemplo, la relación “mayor o igual que” es antisimétrica: si A ≥ B y A ≠ B, entonces no puede cumplirse que B ≥ A. Sin embargo, esta misma relación no es asimétrica, ya que si A = B, tanto A ≥ B como B ≥ A son verdaderos, lo que da lugar a un par simétrico.

Las relaciones antisimétricas forman una subclase dentro de las relaciones definidas en un conjunto.

Un Ejemplo Concreto

Consideremos el conjunto:

$$ I = \{ 1, 2, 3, 4 \} $$

Definimos la relación R como “x es mayor o igual que y”:

$$ R = \{ (4;3), (4;2), (4;1), (3;2), (3;1), (2;1) \} $$

Esta relación es antisimétrica porque, para todo par de elementos distintos x e y, si x ≥ y, entonces y ≥ x no se cumple.

Nota. Por ejemplo, 4 ≥ 3: $$ 4 > 3 $$ pero la inversa, 3 ≥ 4, es falsa: $$ 3 < 4 $$ Por lo tanto, la relación satisface la condición de antisimetría.

En una representación gráfica, ningún par de nodos distintos aparece conectado por aristas en ambos sentidos.

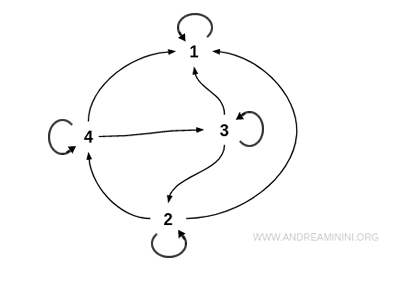
Las únicas conexiones bidireccionales corresponden a bucles, que representan elementos relacionados consigo mismos - por ejemplo, 3 ≥ 3.

A diferencia de lo que ocurre en las relaciones asimétricas, los bucles son perfectamente compatibles con la antisimetría.

Esto se debe a que la antisimetría se refiere exclusivamente a las relaciones entre elementos distintos.

Observaciones Adicionales

Algunas consideraciones relevantes sobre las relaciones antisimétricas:

• Una relación puede no ser ni simétrica ni antisimétrica. Estas propiedades no son excluyentes ni exhaustivas.

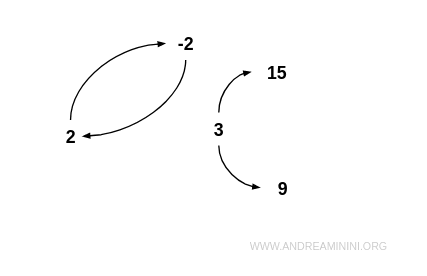
  Ejemplo. Consideremos el conjunto $$ I = \{ -2, 2, 3, 9, 15 \} $$ y la relación R definida como “x es un divisor propio de y”: $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ Esta relación no es antisimétrica, ya que -2 y 2 están relacionados mutuamente. Tampoco es simétrica, pues 9 no es divisor de 3. Por lo tanto, R no es ni simétrica ni antisimétrica. En el grafo correspondiente, se observa una conexión bidireccional entre -2 y 2, pero no en todos los pares de nodos.
  

Y así sucesivamente.