Relaciones Asimétricas

¿Qué es una relación asimétrica?

Una relación definida sobre un conjunto X se dice asimétrica si, cada vez que un elemento a está relacionado con un elemento b, entonces b no está relacionado con a. $$ a R b \ \ \Rightarrow b \require{cancel} \cancel{R} a $$

En una relación asimétrica, ningún par de elementos distintos puede estar relacionado de forma recíproca.

Por ejemplo, la relación “A es madre de B” es asimétrica: si A es madre de B, entonces B no puede ser madre de A.

Las relaciones asimétricas pertenecen al conjunto más amplio de relaciones definidas en un conjunto.

Un Ejemplo Práctico

Consideremos el conjunto:

$$ I = \{ 1, 2, 3, 4 \} $$

Definimos R como la relación “x es mayor que y”:

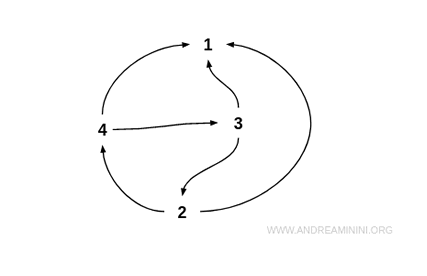
$$ R = \{ (4;3), (4;2), (4;1), (3;2), (3;1), (2;1) \} $$

Esta relación es asimétrica porque si x es mayor que y, entonces y no puede ser mayor que x.

Nota. Por ejemplo, 4 es mayor que 3: $$ 4 > 3 $$ pero 3 no es mayor que 4: $$ 3 < 4 $$ Por lo tanto, la relación cumple la condición de asimetría.

En una representación mediante grafo, una relación asimétrica no presenta aristas bidireccionales entre ningún par de nodos distintos.

Asimetría vs. Antisimetría

Los conceptos de asimetría y antisimetría suelen confundirse, aunque describen propiedades distintas.

• Relación antisimétrica
• En una relación antisimétrica, dos elementos pueden estar relacionados mutuamente solo si son idénticos. Formalmente: si \( aRb \) y \( bRa \), entonces \( a = b \). Es decir, si \( a \ne b \), necesariamente \( b \not\!Ra \). $$ aRb ,\ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$
• Relación asimétrica
• Una relación asimétrica, en cambio, excluye toda forma de reciprocidad, incluso entre elementos iguales. Ni siquiera el par \( (a,a) \) puede pertenecer a la relación. $$ aRb \ \ \Rightarrow b \require{cancel} \cancel{R} a $$

En resumen: la antisimetría permite la reciprocidad solo cuando los elementos coinciden, mientras que la asimetría la prohíbe por completo.

Observaciones Adicionales

Algunas consideraciones importantes sobre las relaciones asimétricas:

• No todas las relaciones son simétricas o asimétricas. Que una relación no sea asimétrica no implica que sea simétrica, y viceversa.

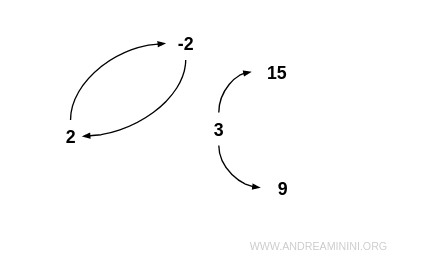
  Ejemplo. Consideremos el conjunto $$ I = \{ -2, 2, 3, 9, 15 \} $$ y la relación R definida como “x es un divisor propio de y”: $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ Esta relación no es asimétrica, ya que -2 y 2 están relacionados en ambos sentidos. Tampoco es simétrica, porque no todas las relaciones son recíprocas: por ejemplo, 3 está relacionado con 9, pero 9 no lo está con 3. Por tanto, R no es ni simétrica ni asimétrica. En el grafo, aparece una conexión bidireccional entre -2 y 2, pero no entre todos los pares de nodos.
  

Y así sucesivamente.