Partición de un Conjunto

partición P(A)

ningún subconjunto es un conjunto vacío
la unión de todos los subconjuntos es igual a A
los subconjuntos son mutuamente excluyentes, es decir, no tienen elementos en común (son disjuntos)

Dividir un conjunto en dos subconjuntos se conoce como bipartición.

Si se divide en tres subconjuntos, se llama tripartición.

En general, una partición en k subconjuntos se denomina una k-partición.

Nota: No hay una única forma de particionar un conjunto. Un conjunto de k elementos puede dividirse en k! particiones distintas.

Un Ejemplo Práctico
Cálculo del Número de Particiones
Observaciones

Un Ejemplo Práctico

Supongamos que tenemos el conjunto finito A con 5 elementos:

$$ A = \{ 1,2,3,4,5 \} $$

Un ejemplo de partición es la siguiente bipartición:

$$ P(A) = \{ \ \{ 1,2,3 \} \ , \ \{ 4,5 \} \ \} $$

Si representamos esta bipartición con diagramas de Euler-Venn, se vería así:

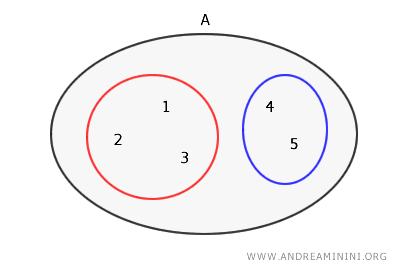
ejemplo de bipartición

Verificación: La partición está formada por dos subconjuntos no vacíos {1,2,3} y {4,5}, que son disjuntos: $$ \{ 1,2,3 \} \cap \{4,5 \} = Ø $$ La unión de ambos subconjuntos es igual a A: $$ \{ 1,2,3 \} \cup \{4,5 \} = \{ 1,2,3,4,5 \} = A $$

Como el conjunto A tiene 5 elementos, existen 52 particiones posibles.

Por ejemplo, otra bipartición posible es:

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4,5 \} \ \} $$

Otro ejemplo es la siguiente tripartición:

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4 \} \ , \ \{ 5 \} \ \} $$

También podemos dividir A en 4 subconjuntos:

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3 \} \ , \ \{ 4 \} \ , \ \{ 5 \} \ \} $$

En total, hay 52 maneras distintas de particionar los elementos del conjunto A.

Cálculo del Número de Particiones

El número de particiones de un conjunto finito $ A $ con $ n $ elementos está dado por el número de Bell $ B_n $. Se puede calcular mediante la siguiente fórmula recursiva, donde $ B_0 = 1 $ es la condición inicial:

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

En esta expresión:

$ \binom{n-1}{k} $ es un coeficiente binomial que indica de cuántas formas se pueden elegir $ k $ elementos de un conjunto de $ n-1 $ elementos.
$ B_k $ representa el número de Bell ya calculado para conjuntos de $ k $ elementos.

El número de Bell $ B_n $ indica, por tanto, la cantidad de formas distintas en que un conjunto de $ n $ elementos puede dividirse en subconjuntos disjuntos.

También puede calcularse mediante la fórmula exponencial de Dobinski:

$$ B_n = \frac{1}{e} \sum_{k=0}^{\infty} \frac{k^n}{k!} $$

Sin embargo, en la práctica suele utilizarse la fórmula recursiva, que permite calcular $ B_5 = 52 $ para el conjunto $ A = \{1,2,3,4,5\} $.

Ejemplo

Vamos a calcular el número de particiones del conjunto $ A $, que contiene $ n = 5 $ elementos:

$$ A = \{ 1,2,3,4,5 \} $$

Para ello, utilizaremos la siguiente fórmula recursiva:

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

En nuestro caso, con $ n=5 $:

$$ B_5 = \sum_{k=0}^{5-1} \binom{5-1}{k} B_k $$

$$ B_5 = \sum_{k=0}^{4} \binom{4}{k} B_k $$

Partimos del valor inicial de la sucesión:

$$ B_0 = 1 $$

Ahora, calculemos $ B_1 $:

$$ B_1 = \sum_{k=0}^{0} \binom{0}{k} B_k = \binom{0}{0} B_0 $$

En este caso, la suma solo tiene un término, ya que el único valor posible de $ k $ es 0.

$ \binom{0}{0} = 1 $, ya que solo hay una manera de elegir 0 elementos de un conjunto vacío.
$ B_0 = 1 $, según la definición inicial.

Por lo tanto:

$$ B_1 = 1 \times 1 = 1 $$

Sigamos con $ B_2 $:

$$ B_2 = \sum_{k=0}^{1} \binom{1}{k} B_k = \binom{1}{0} B_0 + \binom{1}{1} B_1 $$

Calculamos cada término:

$ \binom{1}{0} = 1 $, ya que solo hay una manera de elegir 0 elementos de 1.
$ \binom{1}{1} = 1 $, ya que solo hay una forma de elegir 1 elemento de 1.

Reemplazando los valores de $ B_0 $ y $ B_1 $:

$$ B_2 = 1 \times 1 + 1 \times 1 = 1 + 1 = 2 $$

Continuemos con $ B_3 $:

$$ B_3 = \sum_{k=0}^{2} \binom{2}{k} B_k = \binom{2}{0} B_0 + \binom{2}{1} B_1 + \binom{2}{2} B_2 $$

Evaluamos cada coeficiente binomial:

$ \binom{2}{0} = 1 $, ya que solo hay una forma de elegir 0 elementos de 2.
$ \binom{2}{1} = 2 $, ya que hay dos formas de elegir 1 elemento de 2.
$ \binom{2}{2} = 1 $, ya que solo hay una forma de elegir 2 elementos de 2.

Reemplazando los valores de $ B_0 $, $ B_1 $ y $ B_2 $:

$$ B_3 = 1 \times 1 + 2 \times 1 + 1 \times 2 = 1 + 2 + 2 = 5 $$

Ahora calculemos $ B_4 $:

$$ B_4 = \sum_{k=0}^{3} \binom{3}{k} B_k = \binom{3}{0} B_0 + \binom{3}{1} B_1 + \binom{3}{2} B_2 + \binom{3}{3} B_3 $$

Calculamos cada coeficiente:

$ \binom{3}{0} = 1 $
$ \binom{3}{1} = 3 $, ya que hay tres formas de elegir 1 elemento de 3.
$ \binom{3}{2} = 3 $, ya que hay tres formas de elegir 2 elementos de 3.
$ \binom{3}{3} = 1 $

Reemplazando los valores de $ B_0 $, $ B_1 $, $ B_2 $ y $ B_3 $:

$$ B_4 = 1 \times 1 + 3 \times 1 + 3 \times 2 + 1 \times 5 = 1 + 3 + 6 + 5 = 15 $$

Finalmente, calculemos $ B_5 $:

$$ B_5 = \sum_{k=0}^{4} \binom{4}{k} B_k = \binom{4}{0} B_0 + \binom{4}{1} B_1 + \binom{4}{2} B_2 + \binom{4}{3} B_3 + \binom{4}{4} B_4 $$

Calculamos cada coeficiente:

$ \binom{4}{0} = 1 $
$ \binom{4}{1} = 4 $, ya que hay cuatro formas de elegir 1 elemento de 4.
$ \binom{4}{2} = 6 $, ya que hay seis formas de elegir 2 elementos de 4.
$ \binom{4}{3} = 4 $
$ \binom{4}{4} = 1 $

Reemplazando los valores de $ B_0 $, $ B_1 $, $ B_2 $, $ B_3 $ y $ B_4 $:

$$ B_5 = 1 \times 1 + 4 \times 1 + 6 \times 2 + 4 \times 5 + 1 \times 15 = 1 + 4 + 12 + 20 + 15 = 52 $$

Por lo tanto, el número de Bell para $ n = 5 $ es $ B_5 = 52 $.

En conclusión, hay 52 maneras distintas de particionar el conjunto $ A = \{ 1,2,3,4,5 \} $. Hemos obtenido este resultado aplicando la fórmula recursiva y utilizando coeficientes binomiales.

Observaciones

La partición trivial
Todo conjunto X tiene una partición trivial, que es el propio conjunto en su totalidad: $$ P(A) = \{ A \} $$
Ejemplo: Si tomamos el conjunto $$ A = \{ 1,2,3,4,5 \} $$ su partición trivial sería simplemente: $$ P(A) = \{ \ \{ 1,2,3,4,5 \} \ \} $$
La partición en elementos individuales
También podemos particionar un conjunto en subconjuntos de un solo elemento (conjuntos unitarios o singletons): $$ P(A) = \{ \{ a_1 \} , \{ a_2 \} , ... \} $$
Ejemplo: Para el conjunto $$ A = \{ 1,2,3,4,5 \} $$ la partición en elementos individuales sería: $$ P(A) = \{ \ \{ 1 \} \ , \{ 2 \} \ , \{ 3 \} \ , \{ 4 \} \ , \{ 5 \} \ \} $$

Y así sucesivamente.