Diferencia entre conjuntos abiertos y cerrados

Los conceptos de conjuntos abiertos y cerrados son fundamentales para comprender la estructura de los espacios topológicos. La diferencia principal radica en si el conjunto incluye o no sus puntos de frontera.

Un conjunto cerrado contiene todos sus puntos de frontera, mientras que un conjunto abierto no.

En otras palabras, los puntos de la frontera de un conjunto cerrado pertenecen al conjunto, mientras que en un conjunto abierto quedan fuera de él.

A continuación, se explica cada concepto con más detalle:

• Conjunto Abierto

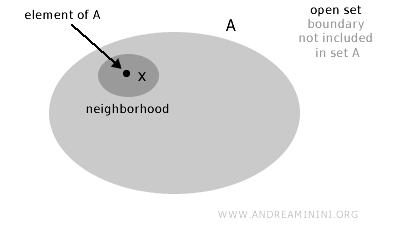
  Un conjunto abierto es aquel que no contiene sus puntos de frontera.

  Más formalmente, un conjunto \(A\) en un espacio topológico \(X\) se considera abierto si, para cada punto \(x\) en \(A\), existe un entorno completamente contenido dentro de \(A\). Es decir, alrededor de cada punto del conjunto es posible encontrar una "vecindad" que permanece íntegramente dentro del conjunto, sin tocar su frontera.
  

  Ejemplo. Un caso sencillo de conjunto abierto es el intervalo \( (3,10) \) en los números reales. Este conjunto está formado por todos los números reales que cumplen \( 3<x<10 \), pero no incluye los extremos 3 y 10. Dichos valores no pertenecen al intervalo, lo que hace que sea un ejemplo típico de conjunto abierto en una dimensión.
  

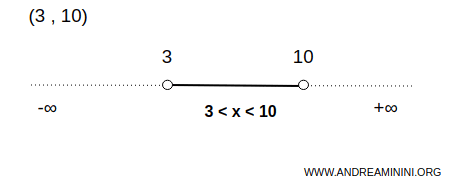
• Conjunto Cerrado

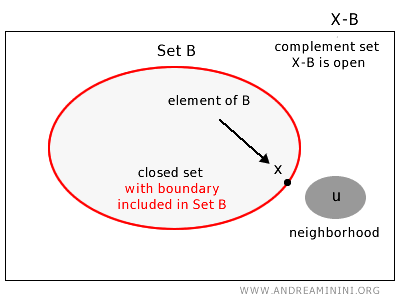
  Un conjunto cerrado es aquel que contiene todos sus puntos de frontera.

  En términos formales, un conjunto \(B\) en un espacio topológico \(X\) es cerrado si su complemento en \(X\), es decir, el conjunto de todos los puntos \(u \in X\) que no pertenecen a \(B\), es un conjunto abierto. Otra propiedad clave de los conjuntos cerrados es que contienen todos sus puntos de acumulación.
  

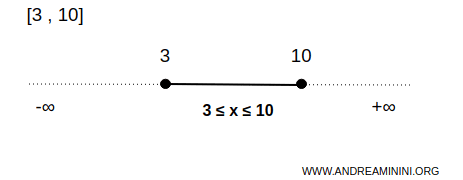
  Ejemplo. Retomemos el ejemplo del intervalo en los números reales. Si ahora consideramos el intervalo cerrado \( [3,10] \), este incluye todos los números tales que \( 3\leq x\leq 10 \), pero, a diferencia del intervalo abierto, también contiene los extremos 3 y 10. En este caso, los puntos 3 y 10 son parte del conjunto y, por lo tanto, cualquier entorno de estos puntos contendrá elementos de \( B \). Por ejemplo, el intervalo simétrico \( 3\pm0.01 \) contiene valores menores que 3 (como 2.99), que no pertenecen a \( B \), lo que confirma que la frontera del conjunto está incluida en él. Este es un ejemplo clásico de conjunto cerrado en una dimensión.
  

¿Por qué es importante distinguir entre conjuntos abiertos y cerrados?

La distinción entre conjuntos abiertos y cerrados es fundamental en diversas ramas de las matemáticas, como el análisis funcional, la geometría diferencial y la teoría de grupos topológicos. Comprender estos conceptos permite caracterizar con precisión la estructura interna de los espacios y definir propiedades esenciales como la continuidad y la compacidad.

Observaciones

Algunas notas adicionales:

• Conjuntos clopen y conjuntos que no son ni abiertos ni cerrados
  En ciertos espacios topológicos, un conjunto puede ser simultáneamente abierto y cerrado. A estos conjuntos se les conoce como "conjuntos clopen". También existen conjuntos que son ni abiertos ni cerrados.

  Por ejemplo, en cualquier espacio topológico, el espacio total y el conjunto vacío siempre son simultáneamente abiertos y cerrados. Estos son los ejemplos más básicos de conjuntos clopen.

Y así sucesivamente.