Conjunto compacto

En un espacio como \(\mathbb{R}^n\), un conjunto compacto es aquel que es simultáneamente cerrado y acotado.

Cerrado: un conjunto es cerrado si contiene todos sus puntos límite, es decir, si incluye todos sus puntos de frontera.
Acotado: un conjunto es acotado si se encuentra completamente contenido dentro de alguna esfera de radio finito.

De manera más general, en un espacio topológico, un conjunto \(K\) es compacto si toda cubierta abierta de \(K\) admite un subcubierta finita que todavía lo recubre por completo.

Estas definiciones son equivalentes en \(\mathbb{R}^n\), pero pueden no coincidir en espacios topológicos más generales.

Nota. La compacidad proporciona una serie de propiedades fundamentales, como garantizar que las funciones continuas alcanzan sus valores máximo y mínimo (Teorema de Weierstrass), y que de toda sucesión puede extraerse siempre una subsucesión convergente (Teorema de Bolzano-Weierstrass). En particular, toda función continua definida en un conjunto compacto necesariamente alcanza sus valores extremo, sin excepciones.

Ejemplos

Ejemplo 1

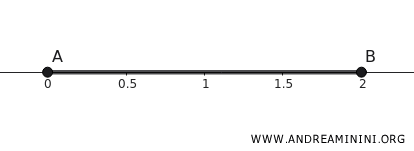
Consideremos el intervalo \([0,2]\) sobre la recta real \(\mathbb{R}\).

Definimos el conjunto:

\[ K = \{ x \in \mathbb{R} \mid 0 \leq x \leq 2 \} \]

Este conjunto es compacto porque:

Es cerrado: contiene los puntos frontera \(0\) y \(2\).
Es acotado: todos sus puntos están comprendidos entre \(0\) y \(2\), por lo que no se extiende indefinidamente.

ejemplo de conjunto compacto

Ejemplo 2

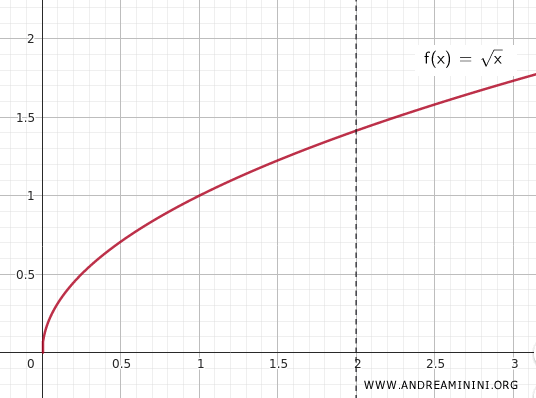
Ahora consideremos la función continua \(f(x) = \sqrt{x}\) definida en \(K\).

Como \(f(x)\) es continua sobre un conjunto compacto, el Teorema de Weierstrass garantiza que alcanza un valor máximo y un valor mínimo en \(K\).

En efecto, sobre el intervalo \([0,2]\), \(f(x)\) alcanza su mínimo en \(x = 0\) (valor \(0\)) y su máximo en \(x = 2\) (valor \(\sqrt{2}\)).

gráfica de una función continua sobre un conjunto compacto

Ejemplo 3

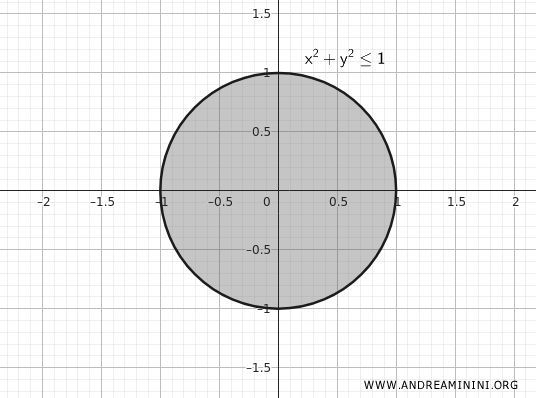
Consideremos ahora el disco cerrado de radio \(1\) centrado en el origen del plano \(\mathbb{R}^2\).

Definimos el conjunto:

\[ K = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 \} \]

Este conjunto también es compacto porque:

Es cerrado: incluye todos los puntos de la circunferencia donde \(x^2 + y^2 = 1\).
Es acotado: ningún punto se encuentra a una distancia mayor que \(1\) del origen \((0,0)\).

disco cerrado que representa un conjunto compacto

Y así sucesivamente.