Distancia entre conjuntos

La distancia entre dos conjuntos $A$ y $B$ en un espacio métrico $(X, d)$ se define como la menor distancia posible entre un punto de $A$ y un punto de $B$: $$ d(A, B) = \inf \{ d(a, b) \mid a \in A \ , \ b \in B \}, $$ donde $d(a, b)$ representa la distancia entre los puntos $a$ y $b$ según la métrica $d$, y $\inf$ denota el ínfimo, es decir, el menor valor dentro del conjunto de todas esas distancias.

Para determinar la distancia entre dos conjuntos, se consideran todos los pares posibles formados por un punto de $A$ y otro de $B$, y se busca la distancia mínima entre ellos.

En definitiva, la distancia entre los conjuntos corresponde al valor más bajo de todas esas distancias.

Nota: La distancia entre conjuntos mide cuán cerca pueden estar entre sí los puntos de ambos conjuntos, pero no implica necesariamente que se toquen ni que coincidan.

¿Cuándo la distancia es cero?

Una distancia igual a cero, $d(A, B) = 0$, indica que existen puntos de $A$ y de $B$ que pueden acercarse indefinidamente entre sí. No obstante, eso no garantiza que los conjuntos se toquen ni que compartan elementos.

Por tanto, es posible que la distancia sea $0$ incluso si los conjuntos son disjuntos, es decir, cuando $A \cap B = \emptyset$.

Un ejemplo práctico

Consideremos dos conjuntos $A$ y $B$ contenidos en un espacio métrico formado por todos los puntos de una recta, donde la distancia se define como $d = |x_1 - x_2|$.

Examinaremos tres casos distintos:

A] Caso 1

Si $A = \{0\}$ y $B = [1, 2]$, entonces la distancia entre ellos sobre la recta numérica es $1$.

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(0, 1) = 1 $$

En este caso, el punto $0$ de $A$ está exactamente a una unidad del punto más próximo de $B$, que es $1$.

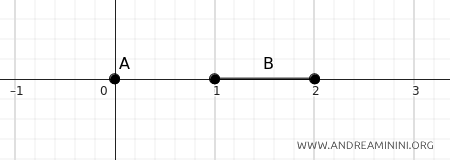
distancia entre un punto aislado y un intervalo cerrado

B] Caso 2

Si $A = [0, 1]$ y $B = [1, 2]$, la distancia entre ambos conjuntos es cero.

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(1, 1) = 0 $$

En este caso, los conjuntos se “tocan” en el punto $1$, por lo que la distancia es $0$.

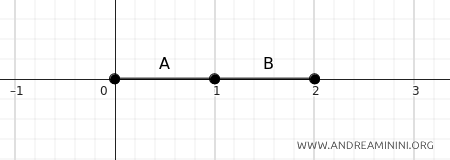
intervalos cerrados que se intersectan en un solo punto

Los conjuntos no son disjuntos, ya que comparten un punto:

$$ A \cap B = \{ 1 \} $$

C] Caso 3

Si $A = (0, 1)$ y $B = (1, 2)$, entonces su distancia también es cero.

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \}. $$

En este caso, $A$ y $B$ son intervalos abiertos que no se intersectan, ya que el punto $1$ no pertenece a ninguno de los dos. Sin embargo, la distancia sigue siendo cero.

$$ A \cap B = \emptyset $$

Esto ocurre porque se pueden tomar puntos $a$ en $A$ y $b$ en $B$ tan cercanos a $1$ como se desee, sin llegar a alcanzarlo, logrando así que la distancia entre ellos se aproxime a cero.

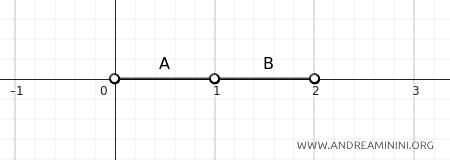
intervalos abiertos que no se tocan pero cuya distancia es cero

El punto $a \in A$ puede aproximarse tanto como se quiera a $1$, pero sin incluirlo, ya que $A$ es un intervalo abierto.

Del mismo modo, los puntos de $B$ pueden acercarse a $1$ desde la derecha, sin incluirlo, por ser también un intervalo abierto.

Por tanto, la distancia entre $A$ y $B$ es:

$$ d(A, B) = \inf \{ |a - b| \mid a \in A, b \in B \} = |1 - 1| = 0 $$

En resumen, aunque $A$ y $B$ no se toquen ni compartan puntos, hay elementos de cada conjunto que pueden acercarse de manera arbitraria entre sí.

Por ello, la distancia entre $A$ y $B$ resulta ser $0$.

Nota: Que la distancia entre dos conjuntos sea igual a $0$ no implica que sean iguales ni que tengan contacto directo. El concepto de distancia se refiere a la cercanía potencial entre sus puntos, no a su intersección.

Y así sucesivamente.