Distancia de Levenshtein

Esta métrica es especialmente útil en aplicaciones como los correctores ortográficos, donde permite comparar palabras similares y proponer sugerencias de corrección. Es una herramienta común para medir la similitud entre cadenas de texto.

Para calcularla, se construye una matriz en la que cada celda representa el coste mínimo de transformar un fragmento de una cadena en un fragmento de la otra, avanzando paso a paso para acumular el menor número de operaciones posible.

A diferencia de la distancia de Hamming, la distancia de Levenshtein también se aplica a cadenas de distinta longitud.

Un ejemplo práctico

Tomemos como ejemplo las cadenas \( s \) y \( t \):

$$ s = "kitten" $$

$$ t = "sitting" $$

Queremos calcular la distancia de Levenshtein entre estas dos palabras, es decir, el número mínimo de ediciones (inserciones, eliminaciones o sustituciones) necesarias para transformar "kitten" en "sitting".

1. Sustitución
   Sustituimos \( k \) por \( s \): $$ "kitten" \rightarrow "sitten" $$
2. Sustitución
   Sustituimos \( e \) por \( i \): $$ "sitten" \rightarrow "sittin" $$
3. Inserción
   Añadimos una \( g \) al final: $$ "sittin" \rightarrow "sitting" $$

En total realizamos tres operaciones (dos sustituciones y una inserción), por lo tanto, la distancia de Levenshtein entre "kitten" y "sitting" es 3.

Para representar este proceso, se construye una matriz de dimensiones \( (m+1) \times (n+1) \), donde \( m \) es la longitud de "kitten" (6) y \( n \) la de "sitting" (7).

Se añaden filas y columnas adicionales para representar las transformaciones desde o hacia una cadena vacía.

	""	s	i	t	t	i	n	g
""	0	1	2	3	4	5	6	7
k	1
i	2
t	3
t	4
e	5
n	6

La celda \( (0, j) \) representa el coste de transformar una cadena vacía en el prefijo de "sitting" de longitud \( j \); por tanto, el valor crece linealmente de 0 a 7.

De forma análoga, la celda \( (i, 0) \) refleja el coste de transformar el prefijo de "kitten" de longitud \( i \) en una cadena vacía, aumentando de 0 a 6.

Para cada celda \( (i, j) \), el valor mínimo se calcula considerando tres posibles operaciones:

1. Eliminar un carácter de "kitten" (costo de la celda superior, \( +1 \))
2. Insertar un carácter en "kitten" (costo de la celda a la izquierda, \( +1 \))
3. Sustituir un carácter (costo de la celda diagonal); si los caracteres coinciden, no se añade coste adicional.

Se procede a completar la matriz paso a paso:

	""	s	i	t	t	i	n	g
""	0	1	2	3	4	5	6	7
k	1	1	2	3	4	5	6	7
i	2	2	1	2	3	4	5	6
t	3	3	2	1	2	3	4	5
t	4	4	3	2	1	2	3	4
e	5	5	4	3	2	2	3	4
n	6	6	5	4	3	3	2	3

Por ejemplo, transformar una cadena vacía en "s", "si", "sit", etc., requiere una operación adicional por cada carácter añadido.

De manera análoga, transformar "k", "ki", "kit", etc., en una cadena vacía implica un coste que aumenta en una unidad por cada carácter eliminado.

• La celda (1,1) muestra el coste de reemplazar "k" por "s", que es 1 porque se requiere una sola sustitución.
  
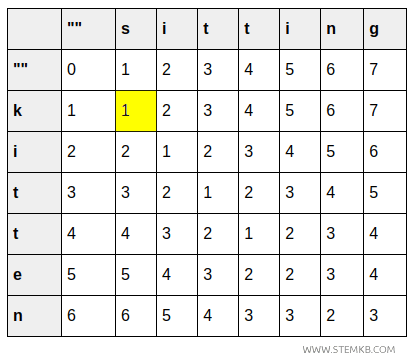
• La celda (2,2) refleja el coste de transformar "ki" en "si", que se mantiene en 1 ya que la segunda letra es idéntica (i).
• La celda (3,3) representa el coste de cambiar "kit" por "sit", que sigue siendo 1 al coincidir la tercera letra (t).
• La celda (4,4) indica el coste de transformar "kitt" en "sitt", también igual a 1 ya que la cuarta letra (t) no cambia.
• La celda (5,5) muestra un coste de 2 al transformar "kitte" en "sitti", debido a una sustitución (e→i).
  
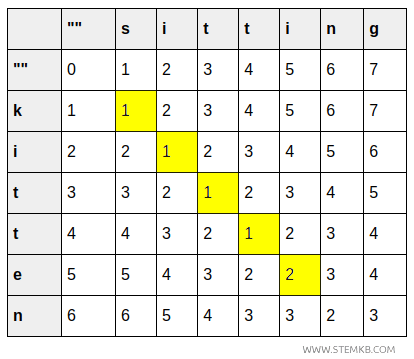
• La celda (6,6) indica el coste de convertir "kitten" en "sittin", que sigue siendo 2, ya que la última letra (n) es la misma.
• La celda (6,7) muestra un coste total de 3 al pasar de "kitten" a "sitting", pues se requiere insertar una letra final (g).
  

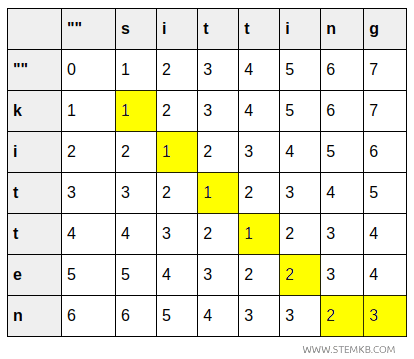
Así, llegamos a la celda final que contiene el coste total acumulado.

La celda inferior derecha \( (6,7) \) recoge el coste mínimo para convertir "kitten" en "sitting": un total de 3.

Ese valor coincide exactamente con la distancia de Levenshtein que calculamos: 2 sustituciones y 1 inserción.

Topología inducida por la distancia de Levenshtein

La distancia de Levenshtein induce una estructura de espacio métrico sobre cadenas de caracteres, de manera análoga a la distancia de Hamming, ya que cumple con las propiedades fundamentales que definen una métrica.

1. No negatividad: La distancia de Levenshtein entre dos cadenas \( x \) e \( y \) es siempre mayor o igual a cero, y \( D_L(x, y) = 0 \) si y solo si \( x = y \). Es decir, no se requieren operaciones para transformar una cadena en sí misma, por lo que la distancia es nula únicamente cuando las cadenas son idénticas.
2. Simetría: La distancia de Levenshtein es simétrica, lo que implica que \( D_L(x, y) = D_L(y, x) \). El número de ediciones necesarias para transformar \( x \) en \( y \) es el mismo que para transformar \( y \) en \( x \), dado que las operaciones permitidas (inserción, eliminación y sustitución) son reversibles.
3. Desigualdad triangular: Se cumple que \( D_L(x, z) \leq D_L(x, y) + D_L(y, z) \). En otras palabras, la distancia directa entre \( x \) y \( z \) nunca excede la suma de las distancias a través de una cadena intermedia \( y \). Esto refleja que cualquier transformación de \( x \) a \( z \) puede descomponerse en pasos que pasan por \( y \).

Gracias a estas propiedades, la distancia de Levenshtein define un espacio métrico sobre el conjunto de cadenas.

Al tratarse de una métrica válida, también podemos considerar la topología métrica inducida asociada a este espacio.

Dado un radio \( r \) y una cadena \( x \), es posible definir una bola abierta centrada en \( x \) como el conjunto de todas las cadenas \( y \) cuya distancia respecto a \( x \) es menor que \( r \):

$$ B(x, r) = \{ y \mid D_L(x, y) < r \} $$

La colección de todas estas bolas abiertas genera los conjuntos abiertos de la topología inducida.

Este enfoque tiene aplicaciones relevantes en dominios donde la noción de “cercanía” entre cadenas es significativa. Por ejemplo, en sistemas de corrección ortográfica automática, una palabra con poca distancia de Levenshtein respecto a otra del diccionario puede ser sugerida como corrección.

En este marco, podemos considerar las cadenas como puntos de un espacio métrico, y utilizar la topología inducida para estudiar su proximidad desde un punto de vista topológico.

Un ejemplo práctico

Consideremos el conjunto \( X \) formado por cadenas de tres caracteres:

$$ X = \{"cat", "bat", "cut"\} $$

Definimos una base para la topología considerando bolas abiertas de radio \( r = 2 \) centradas en cada una de las cadenas de \( X \):

$$ B(x, r) = \{ y \mid D_L(x, y) < r \} $$ 

Cada una de estas bolas abiertas contiene todas las cadenas que difieren en exactamente un carácter respecto a la cadena central, según la distancia de Levenshtein.

Nota: Al emplear un radio \( r = 2 \), se incluyen únicamente las cadenas cuya distancia sea estrictamente menor que 2. En otras palabras, la frontera no pertenece al conjunto, como es habitual en los conjuntos abiertos. Por tanto, $$ B(x, 2) = \{ y \mid D_L(x, y) < 2 \} $$ Para construir conjuntos cerrados que incluyan los puntos en la frontera, se considera la desigualdad \( \leq \): $$ C(x, 2) = \{ y \mid D_L(x, y) \le 2 \} $$

Analizamos ahora las bolas abiertas de radio \( 2 \) centradas en cada elemento de \( X \):

1. Bola abierta centrada en "cat" $$ B("cat", 2) = \{"cat", "bat"\} $$ Estas cadenas se pueden transformar entre sí mediante una única sustitución de carácter, como en los casos “cat” a “bat”, “rat” o “mat”.
2. Bola abierta centrada en "bat" $$ B("bat", 2) = \{"bat", "cat"\} $$ Incluye todas las cadenas transformables en “bat” con un solo paso de edición.
3. Bola abierta centrada en "cut" $$ B("cut", 2) = \{"cut"\} $$ Ninguna otra cadena de \( X \) está a una distancia de una sola edición de “cut”, por lo que esta bola contiene únicamente a sí misma.

Los conjuntos \( B("cat", 2) \), \( B("bat", 2) \) y \( B("cut", 2) \) forman una base para la topología inducida por la distancia de Levenshtein con radio \( r = 1 \).

A partir de esta base, es posible generar todos los demás conjuntos abiertos como uniones arbitrarias de estas bolas abiertas.

Por ejemplo, la unión de \( B("bat", 1) \) y \( B("cut", 1) \) es:

$$ B("bat", 1) \cup B("cut", 1) $$

Dado que \( B("cat", 2) = \{"cat", "bat"\} \) y \( B("cut", 2) = \{"cut"\} \), se tiene:

$$ B("bat", 1) \cup B("cut", 1) = \{"cat", "bat"\} \cup \{"cut"\} $$

$$ B("bat", 1) \cup B("cut", 1) = \{"cat", "bat", "cut"\} $$

Este conjunto también es abierto en la topología inducida.

Mediante esta construcción, obtenemos una topología métrica sobre \( X \) inducida por la distancia de Levenshtein, donde cualquier conjunto abierto puede expresarse como unión de estos elementos básicos.

Y así sucesivamente.