Equivalencia métrica
Dos espacios métricos se consideran equivalentes si existe una función \(f : X \to Y\) que cumple las siguientes condiciones:
- Biyectiva: cada elemento de \(X\) se corresponde con uno y solo un elemento de \(Y\), y viceversa.
- Isométrica: para cualesquiera dos puntos \(x_1, x_2 \in X\), la distancia entre ellos en \(X\) es exactamente igual a la distancia entre sus imágenes \(f(x_1)\) y \(f(x_2)\) en \(Y\). Formalmente: $$ d_X(x_1, x_2) = d_Y(f(x_1), f(x_2)) $$
Cuando existe una función con estas propiedades, decimos que los espacios \(X\) y \(Y\) son isométricos, es decir, métricamente equivalentes.
En términos generales, la equivalencia métrica consiste en comparar dos espacios métricos \((X, d_X)\) y \((Y, d_Y)\) para determinar si son esencialmente iguales en cuanto a la forma en que se mide la distancia entre puntos.
- Si dos espacios métricos son isométricos, entonces comparten la misma topología. Es decir, sus conjuntos abiertos - o la “forma general” del espacio - coinciden. Sin embargo, la implicación contraria no siempre se cumple.
- Compartir la misma topología no garantiza que dos espacios sean isométricos, ya que la isometría impone una condición más estricta que la equivalencia topológica: exige que se conserven exactamente todas las distancias, no solo la estructura de los abiertos.
Un ejemplo práctico
Consideremos los siguientes dos espacios métricos:
- \(X = \{a, b, c\}\), con la métrica \(d_X\) definida por: $$ d_X(a, b) = 1, \quad d_X(b, c) = 2, \quad d_X(a, c) = 3 $$
- \(Y = \{p, q, r\}\), con la métrica \(d_Y\) dada por: $$ d_Y(p, q) = 1, \quad d_Y(q, r) = 2, \quad d_Y(p, r) = 3 $$
Definimos la función \(f : X \to Y\) del siguiente modo:
$$ f(a) = p, \quad f(b) = q, \quad f(c) = r $$
Verifiquemos si conserva las distancias:
- \(d_X(a, b) = 1\), y \(d_Y(f(a), f(b)) = d_Y(p, q) = 1\)
- \(d_X(b, c) = 2\), y \(d_Y(f(b), f(c)) = d_Y(q, r) = 2\)
- \(d_X(a, c) = 3\), y \(d_Y(f(a), f(c)) = d_Y(p, r) = 3\)
Como todas las distancias se conservan, la función \(f\) es una isometría. Por tanto, los espacios \(X\) y \(Y\) son isométricos, es decir, equivalentes desde el punto de vista métrico.
Ejemplo 2
En el plano, la métrica del taxista (\(d_T\)) y la métrica euclidiana estándar (\(d\)) inducen la misma topología: generan los mismos conjuntos abiertos.
Ahora bien, ¿son también isométricos estos dos espacios métricos?
Con la métrica del taxista, la distancia entre dos puntos \((x_1, y_1)\) y \((x_2, y_2)\) se define como:
$$ d_T((x_1, y_1), (x_2, y_2)) = |x_1 - x_2| + |y_1 - y_2| $$
Esta métrica mide la distancia siguiendo trayectorias horizontales y verticales, como si uno se desplazara por una cuadrícula urbana.
En cambio, la métrica euclidiana mide la distancia en línea recta entre dos puntos mediante la fórmula:
$$ d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
Supongamos que existe una función \(f : \mathbb{R}^2 \to \mathbb{R}^2\) que conserva las distancias en ambas métricas. Consideremos los puntos \( A = (1, 1) \) y \( B = (2, 2) \).
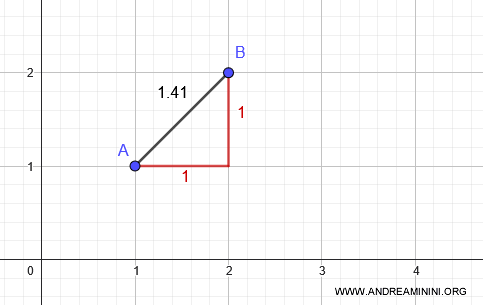
Según la métrica del taxista, la distancia entre estos puntos es:
$$ d_T((2, 2), (1, 1)) = |2 - 1| + |2 - 1| = 2 $$
Mientras que con la métrica euclidiana, obtenemos aproximadamente 1,41:
$$ d((1, 1), (2, 2)) = \sqrt{(1 - 2)^2 + (1 - 2)^2} = \sqrt{2} \approx 1.41 $$
Dado que las distancias difieren, no puede existir una isometría que conserve ambas métricas. Por tanto, el plano con la métrica del taxista no es isométrico al plano con la métrica euclidiana.
En resumen, aunque ambas métricas inducen la misma topología - es decir, comparten los mismos conjuntos abiertos - , no son isométricas.
Y así sucesivamente.