Topología Métrica
La topología métrica en un espacio \( X \) está generada por la base formada por bolas abiertas definidas mediante una distancia \( d \) sobre \( X \). También se conoce como la topología inducida por la métrica \( d \).
En un espacio métrico \( (X, d) \), donde \( d \) es una función que mide la distancia entre puntos de \( X \), podemos definir una topología métrica compuesta por conjuntos abiertos construidos a partir de "bolas abiertas".
Una "bola abierta" centrada en un punto \( x \in X \), con radio positivo \( \varepsilon \), es el conjunto de todos los puntos \( y \in X \) cuya distancia a \( x \) es menor que \( \varepsilon \):
$$ B_d(x, \varepsilon) = \{y \in X \mid d(x, y) < \varepsilon\}. $$
En la topología métrica, un conjunto se considera abierto si puede expresarse como una unión (posiblemente infinita) de estas bolas abiertas.
En otras palabras, un conjunto \( U \subset X \) es abierto en la topología inducida por \( d \) si, para cada punto \( y \in U \), existe un radio \( \delta > 0 \) tal que la bola \( B_d(y, \delta) \) está contenida por completo en \( U \).
Un Ejemplo Práctico
Consideremos el espacio euclídeo unidimensional \(\mathbb{R}\), que esencialmente representa una recta, dotada de la distancia euclídea.
El conjunto \(\mathbb{R}\) está formado por todos los números reales.
La distancia \(d\) entre dos puntos \(x\) e \(y\) en la recta se define como:
$$ d(x, y) = |x - y| $$
Aquí, \(|x - y|\) denota el valor absoluto de la diferencia entre \(x\) e \(y\).
Esta distancia cumple con todas las propiedades que caracterizan a una métrica.
Con esta métrica podemos construir bolas abiertas en \(\mathbb{R}\).
Por ejemplo, tomemos el punto \(x = 3\) y un radio \(\varepsilon = 1\).
La bola abierta centrada en \(x = 3\) con radio \(1\) es:
$$ B_d(3, 1) = \{y \in \mathbb{R} \mid d(3, y) < 1\} = \{y \in \mathbb{R} \mid |3 - y| < 1\} $$
Resolviendo la desigualdad \( |3 - y| < 1 \), obtenemos que \(2 < y < 4\). Por lo tanto:
$$ B_d(3, 1) = (2, 4) $$
Esto significa que la bola abierta centrada en \(3\) con radio \(1\) coincide con el intervalo abierto \((2, 4)\) en la recta real.
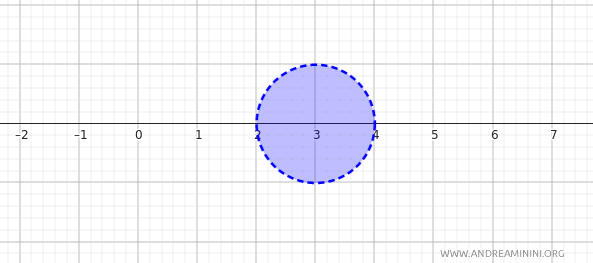
Conjuntos como \( (2, 4) \), \( (5, 7) \), o cualquier intervalo abierto \((a, b)\) de \(\mathbb{R}\), pueden interpretarse como bolas abiertas o uniones de bolas abiertas con respecto a la métrica \(d(x, y) = |x - y|\).
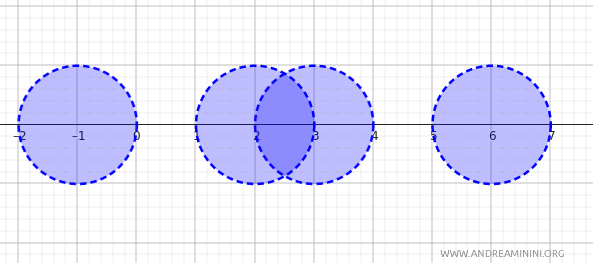
Estos intervalos constituyen una base para la topología métrica en \(\mathbb{R}\).
Nota. En la topología métrica de \(\mathbb{R}\), un conjunto es abierto si, para cada uno de sus puntos, es posible encontrar un intervalo abierto (una bola abierta) que esté completamente contenido en el conjunto. Por ejemplo, \((0, 5)\) es un conjunto abierto porque, para cualquier punto en \((0, 5)\), existe un pequeño intervalo centrado en dicho punto que permanece dentro del conjunto.
En resumen, al emplear la métrica \(d(x, y) = |x - y|\) en \(\mathbb{R}\), se obtiene la topología usual de los intervalos abiertos, la cual se identifica como la topología métrica sobre \(\mathbb{R}\).
Conjuntos Abiertos en la Topología Métrica
En una topología métrica, un subconjunto \( U \subset X \) se define como un conjunto abierto si, para todo punto \( y \in U \), existe una bola abierta centrada en \( y \) - es decir, una "vecindad" con cierto radio \(\delta\) - que esté completamente contenida en \( U \).
En cualquier punto \( y \) de un conjunto abierto \( U \), siempre se puede hallar una pequeña “circunferencia” (o una esfera en dimensiones superiores) que permanezca íntegramente dentro del conjunto.
Esta propiedad es la que caracteriza a los conjuntos abiertos: todo punto del conjunto posee una vecindad que no se extiende fuera de él.
A continuación, se muestra un ejemplo de conjunto abierto en el espacio métrico \( \mathbb{R}^2 \).
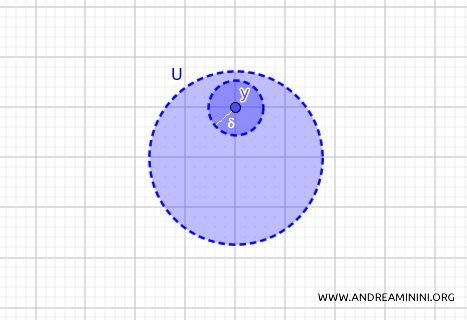
Por contraste, los conjuntos cerrados corresponden a los cierres de bolas abiertas: conjuntos que contienen todos los puntos interiores junto con sus fronteras.
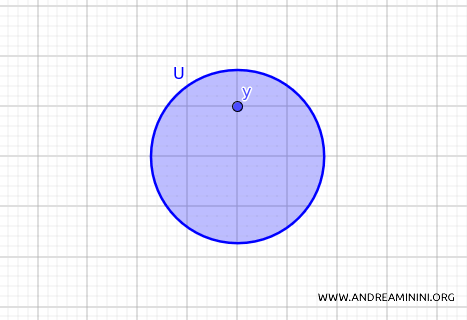
En definitiva, este criterio capta la noción de apertura a través de la “cercanía” interna de cada punto con respecto al conjunto.
Tipos de Métricas
Las topologías inducidas por métricas pueden construirse a partir de distintos tipos de distancia, no únicamente la euclídea (de tipo circular) habitual.
Algunas de las métricas más utilizadas sobre el plano \( \mathbb{R}^2 \) son las siguientes:
- Métrica estándar (o euclídea)
Esta métrica genera conjuntos abiertos con forma circular, conocidos como bolas abiertas en el plano. Define la topología habitual sobre \( \mathbb{R}^2 \). $$ d(p, q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} $$
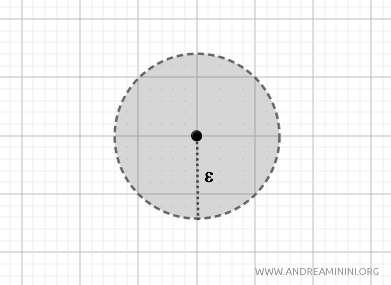
- Métrica del taxi (o distancia Manhattan)
En este caso, las bolas abiertas tienen forma de rombo centrado en \( p \). Esta métrica también induce la topología habitual sobre \( \mathbb{R}^2 \). $$ d_T(p, q) = |p_1 - q_1| + |p_2 - q_2|. $$
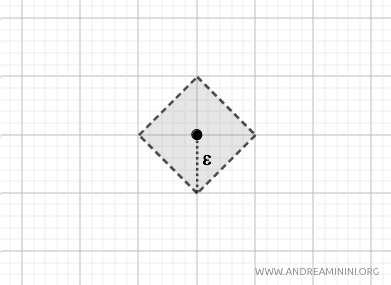
- Métrica del máximo
Con esta métrica, las bolas abiertas son cuadrados centrados en \( p \), con lado de longitud \( 2\varepsilon \). También genera una topología sobre \( \mathbb{R}^2 \).
$$ d_M(p, q) = \max\{|p_1 - q_1|, |p_2 - q_2|\} $$
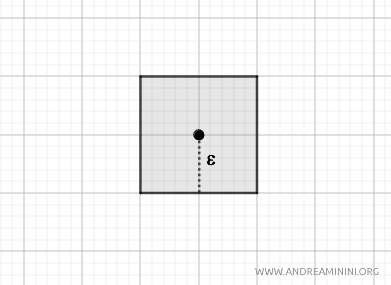
Aunque estas tres métricas generan bolas abiertas con geometrías diferentes (círculo, rombo y cuadrado), todas ellas inducen una topología métrica sobre \( \mathbb{R}^2 \).
Notas Adicionales
A continuación, algunas observaciones complementarias sobre topologías inducidas por métricas:
- Teorema: Comparación de Topologías Métricas
Sean \(d\) y \(d'\) dos métricas definidas sobre un conjunto \(X\), que inducen las topologías \(\mathcal{T}\) y \(\mathcal{T}'\), respectivamente. La topología \(\mathcal{T}'\) es más fina que \(\mathcal{T}\) si y solo si, para todo \(x \in X\) y para cualquier \(\varepsilon > 0\), existe un \(\delta > 0\) tal que: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ donde \(B_{d}(x, \varepsilon)\) y \(B_{d'}(x, \delta)\) son las bolas abiertas centradas en \(x\) con respecto a las métricas \(d\) y \(d'\).
En términos simples, \(\mathcal{T}'\) es más fina que \(\mathcal{T}\) si todo conjunto abierto en la topología inducida por \(d\) contiene al menos un conjunto abierto de la topología inducida por \(d'\). - Teorema de la Métrica Acotada
En un espacio métrico \( (X, d) \), se puede definir una nueva métrica acotada mediante la fórmula \( d'(x, y) = \min(d(x, y), \varepsilon) \), con \(\varepsilon > 0\). Esta métrica genera la misma topología que \( d \), lo cual significa que los conjuntos abiertos inducidos por ambas métricas coinciden.