Teorema de la métrica acotada
En un espacio métrico \( (X, d) \), puede definirse una nueva métrica acotada \( d'(x, y) = \min(d(x, y), 1) \) que induce la misma topología que la métrica original \( d \). Esto significa que los conjuntos abiertos determinados por \( d \) y por \( d' \) coinciden exactamente.
En otras palabras, la métrica \( d'(x, y) \) se obtiene a partir de la métrica original \( d(x, y) \), de modo que:
$$ d'(x, y) = \min(d(x, y), 1) $$
La función \( d' \) coincide con \( d \) mientras \( d(x, y) \lt 1 \), pero si la distancia entre los puntos excede 1, se “recorta” a 1. Así, \( d' \) queda acotada superiormente por ese valor.
A pesar de esta acotación, la topología generada por \( d' \) es idéntica a la inducida por \( d \).
Esto implica que los conjuntos abiertos definidos mediante \( d' \) son exactamente los mismos que los determinados por \( d \), por lo que la estructura topológica del espacio no se ve alterada.
Nota: El valor \(1\) puede sustituirse, en general, por cualquier \(\varepsilon > 0\): $$ d'(x, y) = \min(d(x, y), \varepsilon) $$ En ese caso, las distancias se limitan a \(\varepsilon\), pero la topología generada por \( d' \) sigue siendo la misma que la de \( d \). Para mayor claridad, trabajaremos con el caso particular \(\varepsilon = 1\).
Un ejemplo ilustrativo
Consideremos el espacio \( \mathbb{R} \) con la métrica estándar:
$$ d(x, y) = |x - y| $$
Definimos ahora una nueva métrica acotada de la forma:
$$ d'(x, y) = \min(|x - y|, 1) $$
Con esta definición, ninguna distancia puede superar el valor 1.
Por ejemplo, si \( x = 2 \) y \( y = 5 \), la distancia euclídea es \( d(2, 5) = |2 - 5| = 3 \), mientras que con la métrica acotada se obtiene \( d'(2, 5) = \min(3, 1) = 1 \). En cambio, si \( x = 2 \) y \( y = 2{,}5 \), entonces \( d'(2, 2.5) = \min(|2 - 2.5|, 1) = 0.5 \), lo que coincide con la métrica original, ya que \( |2 - 2.5| \lt 1 \). Así, en este caso, ambas métricas producen el mismo valor: \( d = d' = 0.5 \). $$ \begin{array}{|c|c|c|c|} \hline x & y & d & d' \\ \hline 2 & 5 & 3 & 1 \\ \hline 2 & 2.5 & 0.5 & 0.5 \\ \hline 6 & 8 & 2 & 1 \\ \hline \end{array} $$
La métrica \( d' \) trunca todas las distancias mayores que 1, pero la noción de proximidad - y, con ella, los conjuntos abiertos - permanece inalterada. Por lo tanto, ambas métricas generan exactamente la misma topología.
¿Por qué no cambia la topología?
Los conjuntos abiertos en una topología generada por una métrica se definen como uniones (posiblemente infinitas) de bolas abiertas.
Aunque las bolas abiertas definidas por \( d' \) pueden ser más pequeñas, es posible cubrir cualquier conjunto abierto de \( d \) mediante una cantidad adecuada de bolas abiertas de \( d' \).
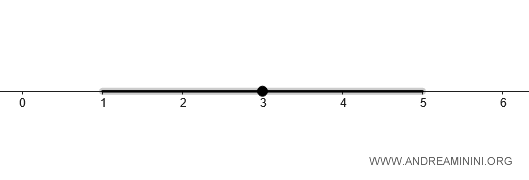
Por ejemplo, consideremos la bola \( B_d(3, 2) \), centrada en \( 3 \) y de radio \( 2 \).
Este conjunto está formado por todos los \( y \in \mathbb{R} \) tales que la distancia entre \( y \) y \( x = 3 \) es menor que \( 2 \):
$$ B_d(3, 2) = \{y \in \mathbb{R} \mid d(3, y) < 2\} $$
Utilizando la métrica estándar \( d(x, y) = |x - y| \), se obtiene:
$$ |3 - y| < 2 \Rightarrow -2 < 3 - y < 2 \Rightarrow 1 < y < 5 $$
Es decir, $$ B_d(3, 2) = (1, 5) $$ un intervalo abierto centrado en \( 3 \) de longitud \( 4 \).
Para cubrir este mismo intervalo usando \( d' \), basta con considerar la unión de bolas más pequeñas, como por ejemplo:
$$ B_{d'}(2, 1) \cup B_{d'}(3, 1) $$
La primera cubre el intervalo \( (1, 3) \), y la segunda \( (2, 4) \); en conjunto, abarcan completamente \( (1, 5) \).
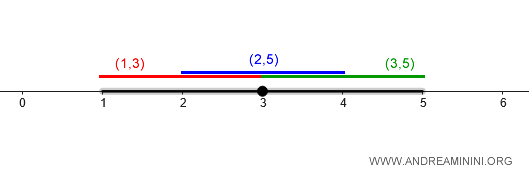
Este ejemplo evidencia que las bolas abiertas de \( d' \), mediante uniones apropiadas, permiten reconstruir cualquier conjunto abierto de \( d \). Por tanto, ambas métricas inducen la misma topología.
Demostración
Para demostrar que \( d' \) induce la misma topología que \( d \), primero comprobamos que \( d' \) cumple con las propiedades de una métrica:
- \( d'(x, y) \geq 0 \) (no negatividad),
- \( d'(x, y) = 0 \) si y solo si \( x = y \) (identidad del indiscernible),
- \( d'(x, y) = d'(y, x) \) (simetría),
- \( d' \) satisface la desigualdad triangular.
La desigualdad triangular se verifica en ambos casos:
- Si \( d(x, y) \geq 1 \) o \( d(y, z) \geq 1 \), entonces \( d'(x, y) + d'(y, z) = 1 + 1 = 2 \), y dado que \( d'(x, z) \leq 1 \), la desigualdad triangular se cumple con holgura.
- Si \( d(x, y) \lt 1 \) y \( d(y, z) \lt 1 \), entonces \( d'(x, y) = d(x, y) \), \( d'(y, z) = d(y, z) \), y \( d'(x, z) = d(x, z) \). Como \( d \) ya es una métrica, la desigualdad triangular se cumple directamente para \( d' \).
Una vez establecida la validez de \( d' \) como métrica, probamos que las topologías inducidas por \( d \) y por \( d' \), que denotamos \( T \) y \( T' \), respectivamente, coinciden. Para ello, basta con verificar:
- \( T \subseteq T' \),
- \( T' \subseteq T \).
A] \( T \subseteq T' \)
Esto se deduce del hecho de que:
- Si \( r \leq 1 \), entonces las bolas son idénticas: $$ B_d(x, r) = B_{d'}(x, r) $$
- Si \( r > 1 \), se cumple que: $$ B_{d'}(x, r) \subseteq B_d(x, r) $$ lo que implica que toda bola abierta de \( d' \) es también abierta en la topología de \( d \).
B] \( T' \subseteq T \)
La inclusión recíproca también es válida, ya que:
- Cuando \( r \leq 1 \), $$ B_d(x, r) = B_{d'}(x, r) $$
- Cuando \( r > 1 \), cualquier bola abierta \( B_d(x, r) \) puede cubrirse mediante un número finito (o infinito) de bolas abiertas más pequeñas en \( d' \), es decir: $$ B_d(x, r) = \bigcup_{i} B_{d'}(x_i, \varepsilon) $$ con \( \varepsilon \leq 1 \).
Conclusión
Dado que cada topología es incluida en la otra, se concluye que son iguales: \( T = T' \), lo que prueba que \( d \) y \( d' \) inducen exactamente la misma estructura topológica sobre \( X \).