Teorema de comparación entre topologías inducidas por métricas

Sean $d$ y $d'$ dos métricas definidas sobre un conjunto $X$, y sean $\mathcal{T}$ y $\mathcal{T}'$ las topologías inducidas por $d$ y $d'$, respectivamente. La topología $\mathcal{T}'$ es más fina que $\mathcal{T}$ si y solo si, para todo $x \in X$ y todo $\varepsilon > 0$, existe un $\delta > 0$ tal que: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ donde $B_d(x, \varepsilon)$ y $B_{d'}(x, \delta)$ denotan bolas abiertas centradas en $x$, con radios $\varepsilon$ y $\delta$, respectivamente, según las métricas $d$ y $d'$.

Dicho de otro modo, si consideramos dos formas distintas de medir distancias en un mismo conjunto $X$ - es decir, dos métricas $d$ y $d'$ - , cada una de ellas genera una topología propia: una colección de conjuntos abiertos.

La topología $\mathcal{T}$, inducida por la métrica $d$
La topología $\mathcal{T}'$, inducida por la métrica $d'$

El teorema afirma que $\mathcal{T}'$ es más fina que $\mathcal{T}$ (es decir, contiene al menos los mismos conjuntos abiertos, y posiblemente más) si y solo si cada conjunto abierto de la topología inducida por $d$ contiene al menos un conjunto abierto perteneciente a la topología inducida por $d'$.

Este enfoque permite clarificar la relación entre ambas topologías y resalta cómo la elección de la métrica influye en la estructura de los conjuntos abiertos.

Un ejemplo práctico
Demostración del teorema

Un ejemplo práctico

Consideremos el conjunto $X = \mathbb{R}^2$, el plano cartesiano, provisto de dos métricas distintas:

Métrica euclídea: $d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$. Las bolas abiertas asociadas a esta métrica son regiones circulares: $$ B_d((x, y), \varepsilon) = \{(u, v) \in \mathbb{R}^2 : \sqrt{(u - x)^2 + (v - y)^2} < \varepsilon\} $$
Métrica discreta: $d'((x_1, y_1), (x_2, y_2)) = \begin{cases} 0 & \text{si } (x_1, y_1) = (x_2, y_2), \\ 1 & \text{si } (x_1, y_1) \neq (x_2, y_2) \end{cases}$. Las bolas abiertas en esta métrica se describen así: \[ B_{d'}((x, y), \delta) = \begin{cases} \{(x, y)\} & \text{si } \delta \leq 1, \\ X & \text{si } \delta > 1. \end{cases} \]

Queremos demostrar que la topología discreta es más fina que la euclídea.

Según el enunciado del teorema:

$$ \mathcal{T}' \text{ es más fina que } \mathcal{T} \iff \forall x \in X, \forall \varepsilon > 0, \ \exists \ \delta > 0 \text{ tal que } B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$

Tomemos un punto arbitrario $P = (x_0, y_0) \in \mathbb{R}^2$ y un radio $\varepsilon > 0$. La bola $B_d(P, \varepsilon)$, en la topología euclídea, es un círculo abierto centrado en $P$ con radio $\varepsilon$.

En la métrica discreta, una bola $B_{d'}(P, \delta)$ se comporta del siguiente modo:

Si $\delta \leq 1$, entonces $B_{d'}(P, \delta) = \{P\}$
Si $\delta > 1$, entonces $B_{d'}(P, \delta) = X$

En esta topología, cada punto del espacio es abierto por sí mismo.

Si tomamos $\delta = 1$, entonces $B_{d'}(P, \delta) = \{P\}$, y como $P \in B_d(P, \varepsilon)$, se cumple que: $$ B_{d'}(P, \delta) \subseteq B_d(P, \varepsilon) $$

Por ejemplo, si elegimos el punto $P = (1, 2) \in \mathbb{R}^2$, en la topología euclídea una bola centrada en $P$ con radio $\varepsilon = 0.4$ es un conjunto abierto.
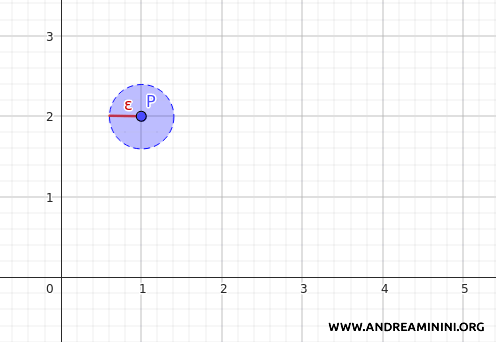
example
En la topología discreta, el conjunto $\{P\} = \{(1, 2)\}$ es abierto por definición. Y como $\{P\} \subseteq B_d(P, \varepsilon)$, se cumple la condición del teorema. Este argumento se puede extender a cualquier otro punto del plano, lo que demuestra que todo conjunto abierto en la topología euclídea contiene al menos un conjunto abierto de la topología discreta.

En conclusión, hemos verificado que se cumple la condición: la topología discreta ($\mathcal{T}'$) es más fina que la euclídea ($\mathcal{T}$), ya que para todo punto $P$ y para cualquier radio $\varepsilon > 0$, existe un $\delta > 0$ (por ejemplo, $\delta = 1$) tal que $B_{d'}(P, \delta) \subseteq B_d(P, \varepsilon)$.

Demostración del teorema

La demostración consiste en establecer la equivalencia lógica en ambas direcciones:

Si $\mathcal{T}'$ es más fina que $\mathcal{T}$, entonces para todo $x \in X$ y todo $\varepsilon > 0$, existe $\delta > 0$ tal que $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$.
Recíprocamente, si dicha inclusión se verifica para todos los puntos y radios, entonces $\mathcal{T}'$ es más fina que $\mathcal{T}$.

La prueba se organiza en dos partes:

A] Primera dirección

Supongamos que la topología $\mathcal{T}'$ es más fina que $\mathcal{T}$. Entonces, para todo $x \in X$ y todo $\varepsilon > 0$, existe $\delta > 0$ tal que $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$.

Por definición, si $\mathcal{T}'$ es más fina que $\mathcal{T}$, entonces todo conjunto abierto en $\mathcal{T}$ también es abierto en $\mathcal{T}'$. En particular, cada bola $B_d(x, \varepsilon)$ es abierta en $\mathcal{T}'$.
Al ser $B_d(x, \varepsilon)$ abierto en $\mathcal{T}'$, debe existir una bola $B_{d'}(x, \delta)$ completamente contenida en él, según la definición de apertura.
Por lo tanto, $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ para algún $\delta > 0$.

B] Segunda dirección

Supongamos ahora que, para todo $x \in X$ y todo $\varepsilon > 0$, existe un $\delta > 0$ tal que $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$. Queremos probar que $\mathcal{T}'$ es más fina que $\mathcal{T}$.

Sea $U$ un conjunto abierto en $\mathcal{T}$. Por definición, $U$ puede expresarse como unión de bolas abiertas $B_d(x, \varepsilon)$.
Tomemos un punto $x \in U$. Entonces existe una bola $B_d(x, \varepsilon) \subseteq U$.
Por hipótesis, existe $\delta > 0$ tal que $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) \subseteq U$.
Esto implica que, para cada punto $x \in U$, existe una bola abierta en la métrica $d'$ contenida en $U$, lo cual demuestra que $U$ es abierto en $\mathcal{T}'$.

Con esto se concluye la demostración de la equivalencia en ambos sentidos.

Y así sucesivamente.