Conjunto Potencia (Conjunto de Todos los Subconjuntos)
¿Qué es el conjunto de todos los subconjuntos?
El conjunto potencia, o conjunto de todos los subconjuntos \( P(A) \), es el conjunto que reúne todos los subconjuntos de \( A \), tanto propios como impropios. $$ P(A) = \{ S | S \subseteq A \} $$ También se conoce como el conjunto potencia.
Cada subconjunto \( S = \{s_1, \dots\} \) es una parte o sección del conjunto \( A \).
$$ S \subseteq A $$
Por lo tanto, cada subconjunto \( S \) es un elemento del conjunto de todos los subconjuntos \( P(A) \).
$$ S \in P(A) $$
Nota. En este caso, el subconjunto es un elemento porque pertenece al conjunto \( P(A) \). Por eso utilizamos la relación de pertenencia \( S \in P(A) \). Sin embargo, \( S \) no está incluido en \( P(A) \), sino en \( A \), es decir, \( S \subseteq A \).
Ejemplo práctico del conjunto de todos los subconjuntos
Consideremos un conjunto \( A \) formado por los elementos \( a \) y \( b \).
$$ A = \{ a,b \} $$
Los elementos \( a \) y \( b \) pertenecen a \( A \).
$$ a,b \in A $$
A continuación, se muestra el diagrama de Venn del conjunto.
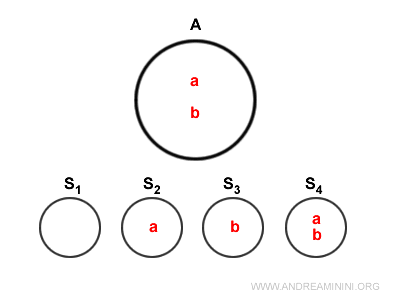
Todos los subconjuntos de \( A \) forman parte del conjunto potencia \( P(A) \).
$$ \{ \} \\ \{ a \} \\ \{ b \} \\ \{ a,b \} $$
Por lo tanto, el conjunto de todos los subconjuntos está compuesto por los siguientes elementos:
$$ P(A) = \{ \{ \} , \{ a \} , \{ b \} , \{ a,b \} \} $$
o expresado de otra forma:
$$ P(A) = \{ ∅ , \{ a \} , \{ b \} , A \} $$
Los subconjuntos \( \{ a \} \) y \( \{ b \} \) son los subconjuntos propios de \( A \).
Mientras que \( ∅ \) y \( A \) son los subconjuntos impropios de \( A \).
Nota. Como todos estos elementos pertenecen a \( P(A) \), también se puede escribir: $$ ∅ , \{ a \} , \{ b \} , A \in P(A) $$
El siguiente es el diagrama de Venn del conjunto potencia \( P(A) \).
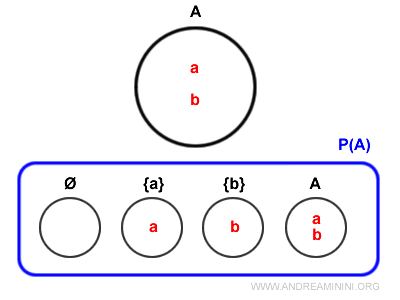
Como puedes ver, incluso el conjunto \( A \) es un elemento de \( P(A) \), ya que todo conjunto es un subconjunto impropio de sí mismo.
¿Por qué también está el conjunto vacío?
En teoría de conjuntos, el conjunto vacío \( ∅ \) es un subconjunto de cualquier conjunto.
Por lo tanto, el conjunto vacío \( ∅ \) también es un subconjunto de \( A \).
Esto significa que \( ∅ \) forma parte del conjunto de todos los subconjuntos \( P(A) \).
El conjunto de todos los subconjuntos del conjunto vacío
Si el conjunto \( A \) es vacío, es decir, \( A = ∅ \), su conjunto potencia es:
$$ P(A) = \{ ∅ \} $$
Es importante aclarar que \( \{∅\} \) no es el conjunto vacío, sino un conjunto que contiene al conjunto vacío como único elemento.
¿Por qué el conjunto de todos los subconjuntos se llama conjunto potencia?
El conjunto de todos los subconjuntos recibe el nombre de conjunto potencia debido a una propiedad fundamental.
Si un conjunto \( A \) tiene \( n \) elementos, su conjunto potencia \( P(A) \) contiene exactamente \( 2^n \) elementos.
Ejemplo
El conjunto \( A = \{a, b\} \) tiene \( n = 2 \) elementos.
Entonces, su conjunto potencia \( P(A) \) contiene 4 elementos:
$$ 2^n = 2^2 = 4 $$
Y este patrón se repite para cualquier conjunto.