Complemento de un Conjunto

Si el conjunto B es un subconjunto de A $$ B⊆A $$, el complemento relativo de B con respecto a A es el conjunto formado por todos los elementos de A que no pertenecen a B. $$ A \text{ \ } B = \{ x \in A | x \notin B \} $$ También se le conoce como el complemento relativo de B en A.

Se lee como "el conjunto A\B es el complemento del conjunto B" o "A\B es el complemento relativo de B en A".

A continuación, se muestra el diagrama de Venn.

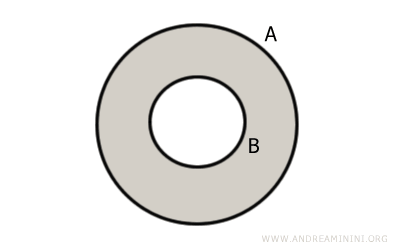
El área en gris representa el complemento de B en A, es decir, el conjunto A\B.

El complemento coincide con la diferencia de conjuntos A-B.

Un Ejemplo Práctico

Veamos un caso concreto con dos conjuntos finitos A y B:

$$ A = \{ 2, 4, 6, 8, 10 \} $$

$$ B = \{ 4, 6 \} $$

El complemento de B con respecto a A está compuesto por los elementos de A que no pertenecen a B:

$$ A \text{ \ } B = A-B = \{ 2, 8, 10 \} $$

Su representación gráfica mediante diagramas de Euler-Venn es la siguiente:

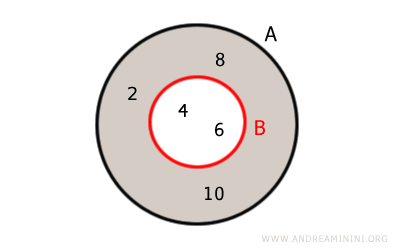
Explicación. Los números 4 y 6 aparecen tanto en A como en B, por lo que son elementos comunes a ambos conjuntos. En cambio, el complemento de B en A está formado por los elementos de A que no están en B, es decir, { 2, 8, 10 }.

Ejemplo 2

Ahora consideremos dos conjuntos infinitos.

El conjunto de los números naturales \( N = \{1, 2, 3, 4, 5, ...\} \) y el subconjunto de los números naturales pares \( P = \{2, 4, 6, 8, ...\} \).

$$ N = \{ 1, 2, 3, 4, 5, ... \ \} $$

$$ P = \{ 2, 4, 6, 8, ... \ \} $$

El complemento de P con respecto a N es el conjunto de los números naturales impares \( D \):

$$ N \text{ \ } P = D = \{ 1, 3, 5, 7, 9, ... \ \} $$

Complemento Absoluto

El complemento absoluto de un conjunto A con respecto al conjunto universal U es el conjunto de todos los elementos de U que no pertenecen a A: $$ C_A = \{ x \in U | x \notin A \} $$ También se le llama el complemento absoluto de A.

¿Qué es el conjunto universal?

El conjunto universal \( U \) es el conjunto que engloba a todos los conjuntos que se están considerando en un determinado contexto.

Si no se especifica lo contrario, el conjunto universal se entiende como el conjunto que contiene todos los elementos posibles dentro del ámbito de estudio.

Ejemplo

Supongamos que tenemos un conjunto \( A \) dentro del conjunto universal \( U \).

El complemento de \( A \), es decir, \( C_A \) (área gris en el diagrama), está formado por todos los elementos de \( U \) que no pertenecen a \( A \) (área blanca).

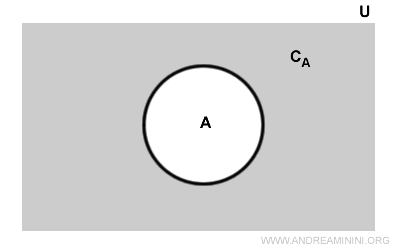
Se dice que "el conjunto U\A (o U-A) es el complemento del conjunto A".

El complemento \( U  \text{ \ }  A \) también puede expresarse mediante las notaciones \( U-A \), \( C_A \), \( A^C \) o \( -A \).

Observaciones

Algunas propiedades útiles de los complementos:

• El complemento de A con respecto a sí mismo es el conjunto vacío, ya que \( A - A = Ø \).

  $$ A \text{ \ } A = A - A = Ø $$

• Si \( A \) y \( B \) son conjuntos iguales (\( A = B \)), su complemento es el conjunto vacío.

  $$ A = B \Longleftrightarrow A - B = Ø $$

• El complemento del conjunto vacío con respecto a \( A \) es el propio \( A \), ya que \( A - Ø = A \).
  

  $$ Ø \text{ \ } A = A $$

• La unión del conjunto \( A \) con el complemento de \( A \) respecto a \( B \) (es decir, \( B \setminus A \)) da como resultado el conjunto \( B \).
  

  $$ A \cup (B \text{ \ } A) = B $$

• La intersección del conjunto \( A \) con su complemento respecto a \( B \) (es decir, \( B \setminus A \)) es el conjunto vacío.
  

  $$ A \cap (B \text{ \ } A) = Ø $$

Y así sucesivamente.