Conjuntos Acotados
¿Qué es un conjunto acotado?
Un conjunto se dice acotado si existe un número real \( M \) tal que todos sus elementos están comprendidos entre \( -M \) y \( +M \). En otras palabras: $$ -M \leq a \leq +M \quad \forall \: a \in A $$ o, de manera equivalente: $$ |a| \leq M \quad \forall \: a \in A $$
Si un conjunto es acotado, significa que está limitado tanto superior como inferiormente.
Demostración
A] Partimos de la desigualdad:
$$ |a| \leq M \quad \forall \: a \in A $$
Por la definición de valor absoluto, esto implica:
$$ -M \leq a \leq M \quad \forall \: a \in A $$
Por lo tanto, \( -M \) es una cota inferior y \( +M \) es una cota superior.
B] Ahora, supongamos que partimos de la desigualdad:
$$ l \leq a \leq L \quad \forall \: a \in A $$
donde \( l \) y \( L \) son números reales. Para establecer una cota general, tomamos:
$$ M = \max(|l|, |L|) $$
Lo que nos permite escribir:
$$ |a| \leq M \quad \forall \: a \in A $$
lo que se traduce en:
$$ -M \leq l \leq a \leq L \leq M \quad \forall \: a \in A $$
Ejemplo Práctico
Consideremos el conjunto de números reales \( A \), compuesto por los siguientes siete elementos:
$$ A = \{ -7, 4, 2, 6, 3, 5, 1 \} $$
Este conjunto tiene infinitas cotas inferiores en el intervalo \( (-\infty, -7] \) y también infinitas cotas superiores en \( [6, +\infty) \).
Para encontrar las cotas más ajustadas, identificamos la mayor cota inferior \( l = -7 \) y la menor cota superior \( L = 6 \).
$$ l = -7, \quad L = 6 $$
A continuación, calculamos \( M \), que es el mayor valor absoluto entre \( l \) y \( L \):
$$ M = \max(|l|, |L|) $$
$$ M = \max( |-7|, |6|) $$
$$ M = \max(7, 6) $$
$$ M = 7 $$
Dado que existe un número real \( M = 7 \) tal que:
$$ -M \leq a \leq M \quad \forall a \in A $$
$$ -7 \leq a \leq 7 \quad \forall a \in A $$
el conjunto \( A \) cumple la condición de acotamiento, lo que confirma que es un conjunto acotado.
Conjuntos Acotados Inferiormente
Un conjunto se dice acotado inferiormente si existe un número real \( M \) tal que todos sus elementos son mayores o iguales a \( M \): $$ a \geq M \quad \forall \: a \in A $$
Un conjunto acotado inferiormente siempre posee al menos una cota inferior.
Si un conjunto está acotado inferiormente, tiene un número finito llamado ínfimo o máxima cota inferior.
En un conjunto no vacío y acotado de números reales, el ínfimo es la mayor de todas las cotas inferiores.
$$ m = \inf(A) = \begin{cases} m \leq a \quad \forall a \in A \\ \\ \forall \epsilon > 0, \: \exists \: a \in A \text{ tal que } m + \epsilon > a \end{cases} $$
Ejemplo: El conjunto de los números reales positivos \( R^+ \) está acotado inferiormente, pues todos sus elementos pertenecen al intervalo \( (0, +\infty) \). Su ínfimo es \( M = 0 \), ya que es la mayor cota inferior. Sin embargo, el conjunto no está acotado superiormente, ya que no tiene un límite finito, por lo que su supremo es \( +\infty \).
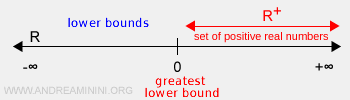
Si un conjunto no está acotado inferiormente, su ínfimo es menos infinito (-∞):
$$ \inf(A) = -\infty \Leftrightarrow \forall \: l \in R, \: \exists \: a \in A \text{ tal que } a < l $$
Conjuntos Acotados Superiormente
Un conjunto está acotado superiormente si existe un número real \( M \) tal que todos sus elementos son menores o iguales a \( M \): $$ a \leq M \quad \forall \: a \in A $$
Un conjunto acotado superiormente siempre tiene al menos una cota superior.
Si un conjunto está acotado superiormente, tiene un número finito llamado supremo o mínima cota superior.
En un conjunto no vacío y acotado de números reales, el supremo es la menor de todas las cotas superiores.
$$ M = \sup(A) = \begin{cases} M \geq a \quad \forall a \in A \\ \\ \forall \epsilon > 0, \: \exists \: a \in A \text{ tal que } M - \epsilon < a \end{cases} $$
Ejemplo: El conjunto de los números reales negativos \( R^- \) está acotado superiormente, ya que todos sus elementos pertenecen al intervalo \( (-\infty, 0) \). Su supremo es \( M = 0 \), pues es la menor cota superior. Sin embargo, el conjunto no está acotado inferiormente, ya que no tiene un límite inferior finito, por lo que su ínfimo es \( -\infty \).
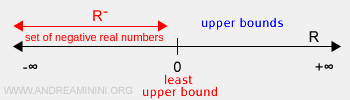
Si un conjunto no está acotado superiormente, su supremo es infinito positivo (+∞):
$$ \sup(A) = +\infty \Leftrightarrow \forall \: L \in R, \: \exists \: a \in A \text{ tal que } a > L $$
Conjunto Acotado en el Plano
Un conjunto \(A \subseteq \mathbb{R}^2\) se denomina acotado en el plano si existe un número real positivo \(M > 0\) y un punto \(P_0\) en el plano tales que, para todo punto \(P\) de \(A\), la distancia entre \(P\) y \(P_0\) es menor que \(M\). \[ \exists \ P_0 \in \mathbb{R}^2, \exists \ M > 0 \text{ tal que } \forall \ P \in A, \quad d(P, P_0) < M \] donde \(d(P, P_0)\) denota la distancia euclidiana.
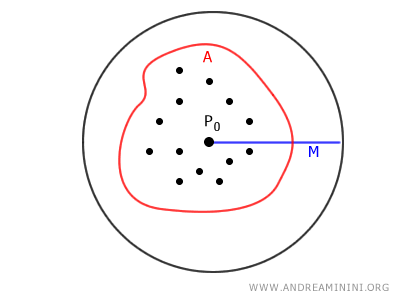
Dicho de otro modo, un conjunto en \(\mathbb{R}^2\) es acotado si todos sus puntos se encuentran contenidos dentro de algún círculo de radio finito.
En términos generales, un conjunto es acotado si no se extiende indefinidamente en ninguna dirección y puede quedar contenido íntegramente en un círculo lo suficientemente grande.
Ejemplos de conjuntos acotados en el plano son:
- Un círculo de radio \(r\), con o sin su borde.
- Un cuadrado, un rectángulo, un triángulo o cualquier otro polígono.
- Cualquier figura cerrada que posea dimensiones finitas.
Nota. En cambio, ejemplos de conjuntos no acotados incluyen una recta, una parábola, una espiral que se expande indefinidamente como \(y = x^2\), o un cuadrante entero del plano cartesiano.