Unión de Conjuntos
La unión de dos conjuntos A y B es el conjunto formado por todos los elementos que pertenecen a A, a B o a ambos.

El símbolo que representa la unión es ∪.
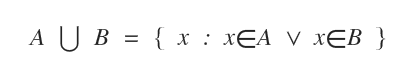
Se lee como unión de A y B o simplemente A unión B.
Si hay elementos en común entre ambos conjuntos, estos solo se cuentan una vez en la unión.
Unión de Múltiples Conjuntos. La operación de unión también puede aplicarse a más de dos conjuntos. Para representar la unión de una familia de conjuntos, se utiliza la notación: $$ \bigcup_{i \in I} = \{ x \in A_i \:\: \text{para algún}\:\: i \in I \} $$
Ejemplo Práctico
Supongamos que tenemos dos conjuntos A y B.
El conjunto A está formado por los elementos { 2, 5, 6, 7, 8 }, mientras que el conjunto B contiene { 1, 3, 4, 6, 7, 9 }.

La unión de A y B se expresa como A ∪ B y resulta en el conjunto { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.
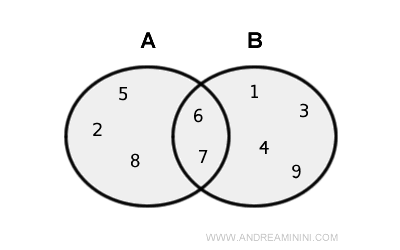
Nota. Los elementos {6, 7} aparecen tanto en A como en B. Sin embargo, en la unión A ∪ B, estos solo se incluyen una vez, ya que en un conjunto no pueden existir elementos repetidos.
Ejemplo 2
Consideremos dos conjuntos A y B:
$$ A = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$
$$ B = \{ 2, 4, 6, 8 \} $$
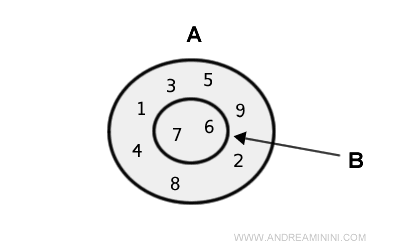
En este caso, B es un subconjunto propio de A.
Por lo tanto, la unión de ambos conjuntos es simplemente el conjunto A.
$$ A \cup B = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$
Los elementos comunes no se repiten en la unión.
Ejemplo 3
Ahora consideremos los conjuntos:
$$ A = \{ 1 , 3, 5, 7, 9 \} $$
$$ B = \{ 2, 4, 6, 8 \} $$
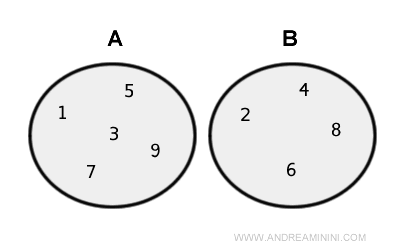
En este caso, los dos conjuntos son disjuntos, es decir, no tienen elementos en común.
Su unión contiene todos los elementos de A y de B.
$$ A \cup B = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$
La siguiente imagen muestra la representación de la unión con diagramas de Euler-Venn.
Nota. La unión de conjuntos se asemeja a la disyunción lógica inclusiva ("OR"). A diferencia de la disyunción exclusiva (XOR), que excluye una de las alternativas, la unión incluye todos los elementos de ambos conjuntos, incluso aquellos que se repiten.
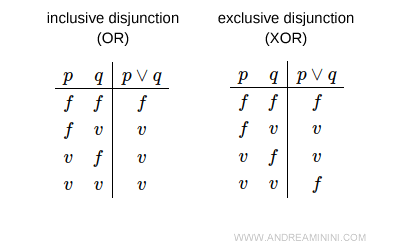
Por eso, cuando se compara la unión con la disyunción lógica, es importante especificar que se trata de la disyunción inclusiva.
Propiedades de la Unión
La unión de conjuntos cumple con ciertas propiedades similares a las de la suma y la multiplicación en aritmética:
- Propiedad conmutativa
El orden de los conjuntos no afecta el resultado: $$ A \cup B = B \cup A $$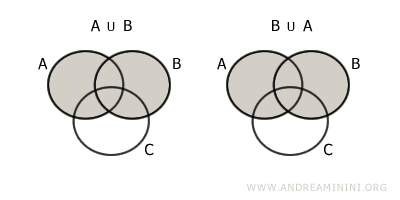
- Propiedad asociativa
La forma de agrupar los conjuntos no cambia la unión: $$ (A \cup B) \cup C = A \cup (B \cup C) $$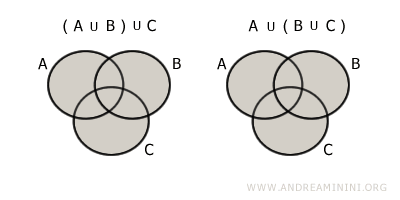
- Propiedad distributiva de la unión sobre la intersección
La unión de un conjunto con la intersección de otros dos es equivalente a la intersección de sus uniones:$$ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) $$
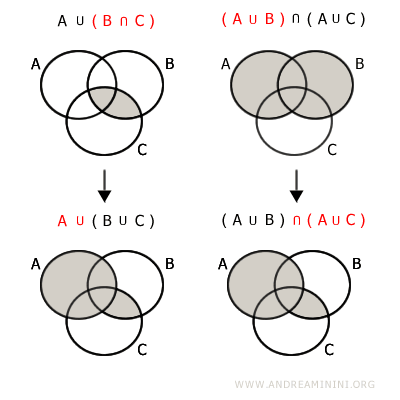
Cardinalidad de la Unión
La cardinalidad de la unión depende de si los conjuntos tienen elementos en común o no.
- Conjuntos disjuntos
Si no hay elementos en común, la cardinalidad de la unión es la suma de las cardinalidades individuales: $$ |A\cup B|=|A| + |B| $$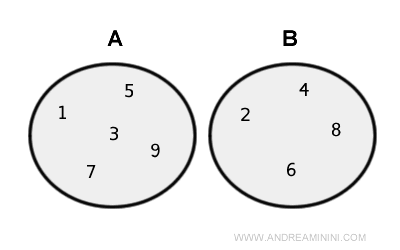
- Conjuntos con elementos en común
Cuando los conjuntos comparten elementos, la cardinalidad de la unión se obtiene restando la intersección: $$ |A\cup B|=|A| + |B| - |A\cap B| $$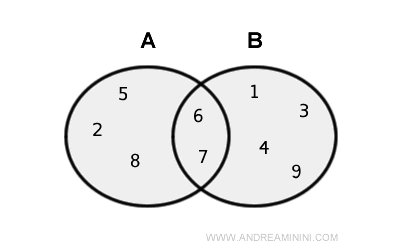
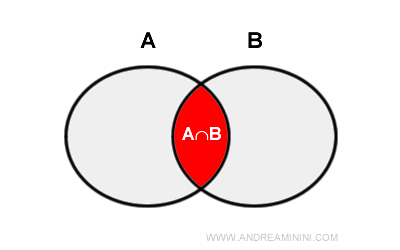
Explicación. Al sumar los elementos de ambos conjuntos, los elementos de la intersección A⋂B se cuentan dos veces. Para obtener la cardinalidad correcta de la unión A ∪ B, es necesario restar una vez los elementos que aparecen en la intersección A⋂B, evitando así duplicaciones.
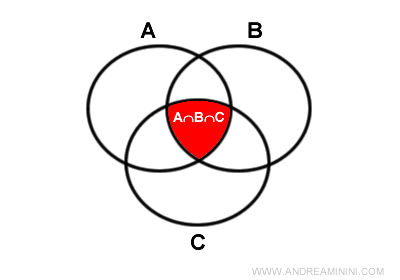
Si en lugar de dos conjuntos tenemos tres conjuntos no disjuntos, la cardinalidad de su unión se determina aplicando el principio de inclusión-exclusión:
$$ |A\cup B\cup C| = |A| + |B| + |C| - |A\cap B| - |A\cap C| - |B\cap C| + |A\cap B\cap C| $$
En este caso, las intersecciones de dos conjuntos se han contado dos veces en la suma inicial, por lo que es necesario restarlas una vez. Sin embargo, la intersección de los tres conjuntos A⋂B⋂C se ha restado en exceso, por lo que debemos sumarla nuevamente para corregir el resultado.
Explicación. Al sumar |A| + |B| + |C|, los elementos que pertenecen a las intersecciones |A⋂B|, |A⋂C| y |B⋂C| se cuentan dos veces, mientras que los elementos de la intersección |A⋂B⋂C| se cuentan tres veces. Para corregir esto, primero restamos una vez cada intersección de dos conjuntos. Sin embargo, al hacerlo, los elementos de la intersección |A⋂B⋂C| quedan eliminados en exceso, ya que se han restado tres veces. Por ello, debemos volver a sumarlos una vez para equilibrar la cuenta.
Este principio también se extiende a la unión de más de dos conjuntos, siguiendo la regla de inclusión-exclusión.