Producto Cartesiano
El producto cartesiano es una operación matemática entre dos conjuntos.
Definición
Dado dos conjuntos A y B, el producto cartesiano AxB es el conjunto formado por todos los pares ordenados (a,b), donde el primer elemento "a" pertenece al conjunto A y el segundo elemento "b" pertenece al conjunto B.
En términos matemáticos, el producto cartesiano se expresa de la siguiente manera:
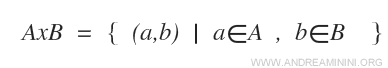
Se lee como "A por B" o "A cartesiano B".
Un Ejemplo Práctico
Para entender mejor el producto cartesiano, veamos un ejemplo concreto.
Supongamos que tenemos dos conjuntos A y B, el primero con dos elementos y el segundo con tres.
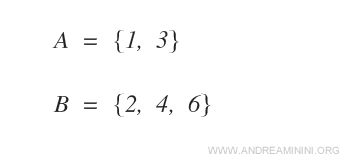
El producto cartesiano AxB es el siguiente conjunto:
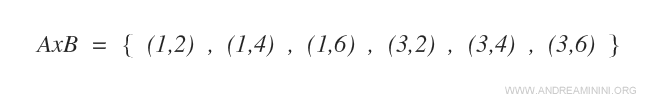
Cada uno de los elementos del producto cartesiano AxB es un par ordenado.
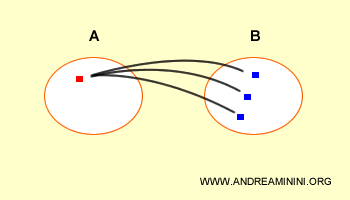
Visualmente, la relación entre ambos conjuntos se representa de la siguiente forma:
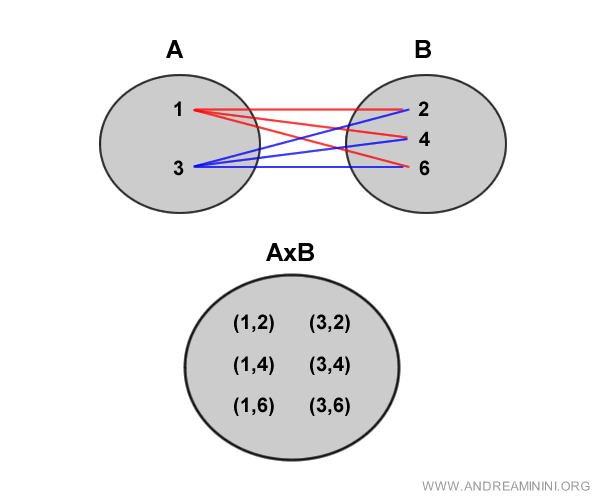
Nota. Los elementos del producto cartesiano no pertenecen ni a A ni a B como elementos individuales, sino que forman una nueva estructura: pares ordenados que combinan elementos de ambos conjuntos.
En un sistema de coordenadas cartesianas, estos pares ordenados pueden representarse como puntos (x, y).
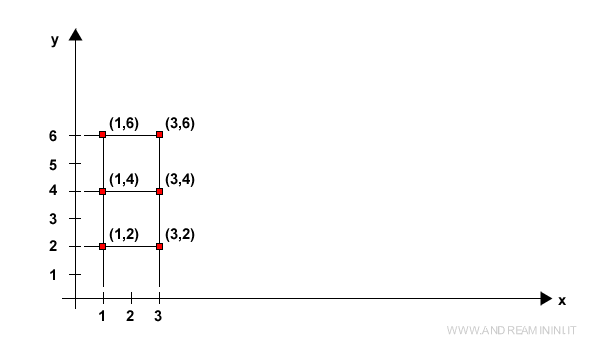
¿Cómo Representar el Producto Cartesiano?
Existen distintas formas de representar el producto cartesiano:
- Diagrama cartesiano
En un sistema de coordenadas, colocamos los elementos del conjunto A en el eje x (horizontal) y los de B en el eje y (vertical). Cada par ordenado (a,b) se traduce en un punto único en el plano cartesiano con coordenadas (x=a, y=b).
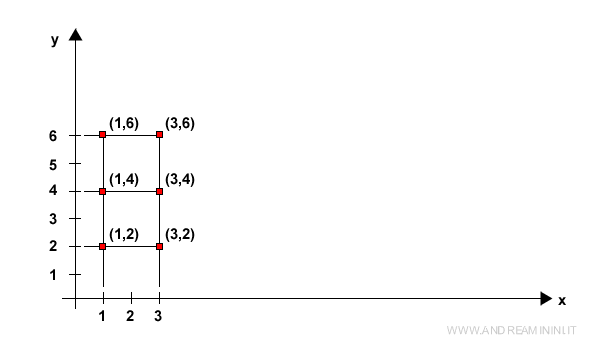
- Tabla de doble entrada
En una tabla, los elementos del conjunto A se colocan en las filas y los del conjunto B en las columnas. En cada celda de la tabla se coloca el par ordenado correspondiente a la intersección de la fila y la columna.
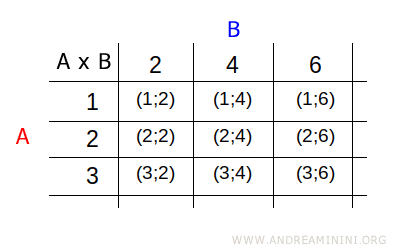
Nota. Esta representación es especialmente útil cuando los conjuntos contienen elementos que no son números.
¿Qué es un Par Ordenado?
Un par ordenado (a,b) es una pareja de elementos en la que el orden importa: el primer elemento es "a" y el segundo es "b".
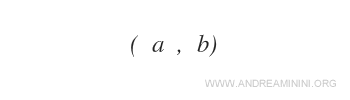
Se representan usando paréntesis y separando los elementos con una coma.
Es posible que ambos elementos sean iguales.
El orden es fundamental
El orden de los elementos en un par ordenado no es intercambiable.
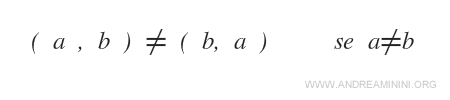
Ejemplo
Los pares (2,4) y (4,2) son distintos, ya que aunque contienen los mismos números, el orden cambia su significado.
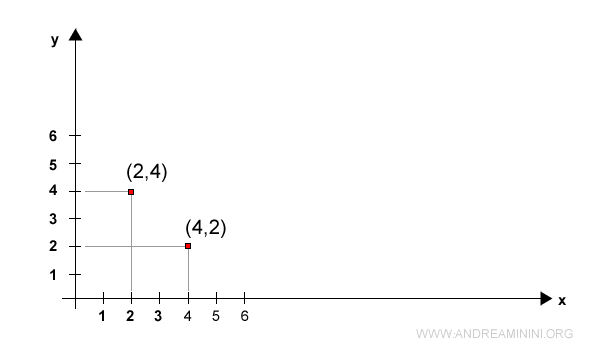
¿Cuándo son iguales dos pares ordenados?
Dos pares ordenados (a,b) y (c,d) son iguales únicamente si sus elementos coinciden en el mismo orden, es decir, si el primer elemento del primer par es igual al primer elemento del segundo par (a=c) y el segundo elemento del primer par es igual al segundo elemento del segundo par (b=d).
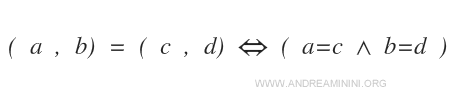
La Propiedad Conmutativa del Producto Cartesiano
El producto cartesiano no es conmutativo.
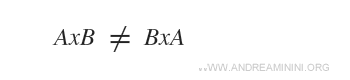
Ejemplo
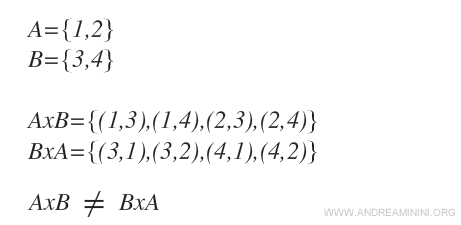
Es evidente que AxB ≠ BxA, ya que, a diferencia de un conjunto, en un par ordenado el orden de los elementos es esencial.
Esta diferencia se vuelve más clara cuando representamos ambos productos cartesianos en un diagrama cartesiano.
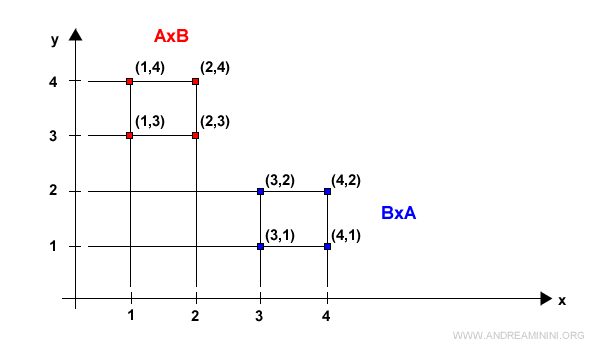
Nota. La única situación en la que AxB = BxA ocurre cuando A = B. Si los dos conjuntos son idénticos, el producto cartesiano sí cumple con la propiedad conmutativa.

La Propiedad Distributiva
El producto cartesiano satisface la propiedad distributiva con respecto a la unión e intersección de conjuntos.
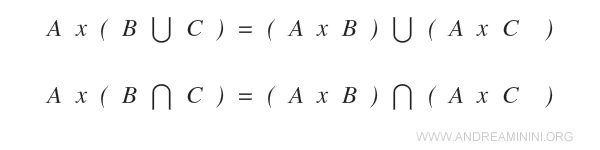
Demostración
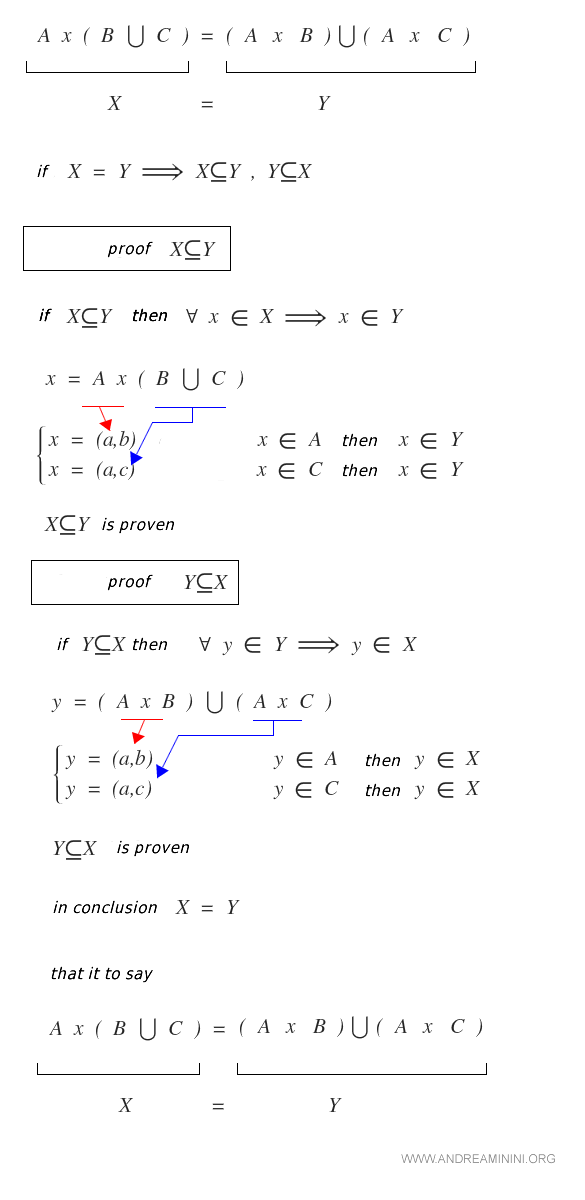
El Producto Cartesiano de un Conjunto Vacío
Si uno de los conjuntos involucrados en el producto cartesiano es vacío, el resultado también será un conjunto vacío.
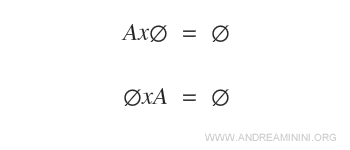
El Producto Cartesiano de n Conjuntos
El producto cartesiano no se limita a dos conjuntos, sino que puede extenderse a un número arbitrario n de conjuntos.
Dado un conjunto de n conjuntos A1, A2,..., An, el producto cartesiano A1xA2x...xAn es el conjunto de todas las n-tuplas (a1, a2,..., an): $$ A_1\:x\:A_2\:x\:...\:x\:A_n = \{ (a_1,a_2,...,a_n) | a_i \in A_i , i=1,2,...,n \} $$
Donde cada elemento ai pertenece al conjunto Ai correspondiente.
El Producto Cartesiano de un Conjunto Consigo Mismo
También es posible calcular el producto cartesiano de un conjunto consigo mismo.
Ejemplo
Consideremos el conjunto A:
$$ A = \{ 1,2,3 \} $$
Su producto cartesiano consigo mismo A×A es el conjunto de pares ordenados:
$$ A×A = \{ (1,1) , (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) \} $$
Este concepto puede extenderse a productos cartesianos de mayor dimensión, generando tríos, cuádruplas o n-tuplas.