Subconjuntos Propios
¿Qué es un subconjunto propio?
- Decimos que un conjunto A es un subconjunto propio de un conjunto B cuando:
- todos los elementos de A también pertenecen a B,
- pero B tiene al menos un elemento que no está en A.
A esto se le llama una relación de inclusión estricta.
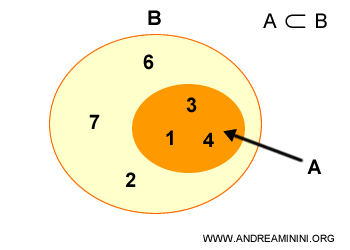
Se trata de un caso particular de inclusión, representado con el símbolo ⊂.
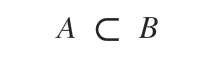
Esta notación se lee como "El conjunto A es una parte propia del conjunto B" o "El conjunto A está estrictamente contenido en el conjunto B".
La inclusión estricta implica que los conjuntos son distintos, es decir, A≠B.
¿Cuál es la diferencia entre inclusión normal e inclusión estricta? En la inclusión estricta (A⊂B), los conjuntos A y B deben ser diferentes (A≠B), ya que B tiene al menos un elemento que no está en A. En cambio, en la inclusión normal (A⊆B), los conjuntos pueden ser idénticos (A=B). Por lo tanto, si A está estrictamente contenido en B (A⊂B), también se cumple la inclusión normal (A⊆B). Sin embargo, si A está incluido en B en sentido normal (A⊆B), esto no implica necesariamente que sea una inclusión estricta, ya que A y B podrían ser iguales (A=B).
Ejemplo
El conjunto A tiene tres elementos, mientras que el conjunto B tiene seis.
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4,2,6,7 \} $$
La primera condición para la inclusión estricta se cumple porque todos los elementos de A también están en B.
$$ A = \{ 1,3,4 \} ⊂ B $$
La segunda condición también se cumple, ya que hay al menos un elemento en B que no pertenece a A.
En este caso, los elementos {2,6,7} están en B, pero no en A.
$$ B = \{ 1,3,4,\color{red}2,\color{red}6,\color{red}7 \} $$
Por lo tanto, A está estrictamente contenido en B, es decir, A es un subconjunto propio de B.
$$ A ⊂ B $$
Y así sucesivamente.