Cotas Superior e Inferior

Explorando las Cotas Superior e Inferior

Dado un conjunto A y un subconjunto B⊆A

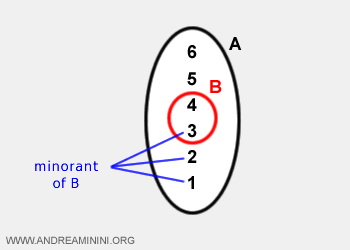
• Un elemento k ∈ A se dice que es una cota inferior (o minorante) del subconjunto B si es menor o igual que todos los elementos de B.

  Ejemplo. Consideremos el conjunto A = {1, 2, 3, 4, 5, 6} y el subconjunto B = {3, 4}. Las cotas inferiores de B son {1, 2, 3}.
  

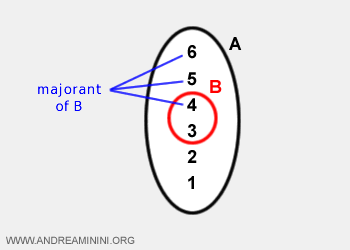
• Un elemento k ∈ A se dice que es una cota superior (o mayorante) del subconjunto B si es mayor o igual que todos los elementos de B.

  Ejemplo. Para el conjunto A = {1, 2, 3, 4, 5, 6} y el subconjunto B = {3, 4}, las cotas superiores de B son {4, 5, 6}.
  

Rango de Cotas Superiores e Inferiores en un Conjunto

Un conjunto puede tener varias cotas superiores e inferiores, o incluso no tener ninguna.

Ejemplos Prácticos

Algunos conjuntos poseen cotas inferiores pero no cotas superiores.

Estos se denominan conjuntos acotados inferiormente.

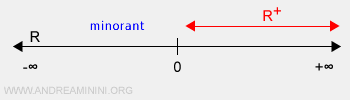
Ejemplo de un conjunto sin cotas superiores. El conjunto de los números reales positivos R⁺, una colección infinita dentro del intervalo (0,+∞), es un subconjunto de los números reales R. Cuenta con cotas inferiores, como el cero y todos los números reales negativos, aunque estas cotas no pertenecen a R⁺ en sí. Por ejemplo, el cero no forma parte de R⁺, y entre cualquier número real positivo y el cero hay infinitos números reales. Además, R⁺ carece de cotas superiores, ya que se extiende indefinidamente hacia +∞.

Por el contrario, hay conjuntos que tienen cotas superiores pero no cotas inferiores.

A estos conjuntos se les llama conjuntos acotados superiormente.

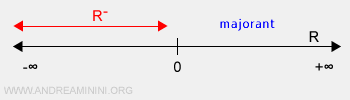
Ejemplo de un conjunto sin cotas inferiores. El conjunto de los números reales negativos R^- es un subconjunto infinito dentro del intervalo (-∞,0), contenido en el conjunto de los números reales R. Tiene cotas superiores, como el cero y todos los números reales positivos, aunque ninguna de ellas pertenece a R^-. Por ejemplo, el cero no está en R^-, y entre cualquier número real negativo y el cero hay infinitos números reales. Además, R^- no tiene cotas inferiores, ya que se prolonga sin límite hacia -∞.

También existen conjuntos que están acotados tanto por arriba como por abajo.

Estos conjuntos se conocen como conjuntos acotados.

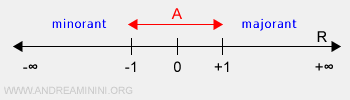
Ejemplo de un conjunto con cotas superior e inferior. El conjunto de los números reales comprendidos entre -1 y +1 es un subconjunto de los números reales R. Este conjunto tiene infinitas cotas inferiores en el intervalo (-∞, -1) y, de igual manera, infinitas cotas superiores en el intervalo (1,+∞).

Por último, existen conjuntos que no tienen ni cotas superiores ni cotas inferiores.

Ejemplo de un conjunto sin cotas. El conjunto vacío es un subconjunto impropio de cualquier otro conjunto universal y carece tanto de cotas superiores como de cotas inferiores. De forma similar, cualquier conjunto que no esté acotado ni por arriba ni por abajo, como el conjunto de los números reales R, es un subconjunto impropio de sí mismo y, por lo tanto, no tiene cotas.

Y así sucesivamente.