Extremos (ínfimo y supremo) de un conjunto
Qué son los extremos
- Todo subconjunto no vacío de los números reales admite un extremo inferior y un extremo superior, que pueden ser finitos o infinitos.
- En los conjuntos acotados, ambos extremos son números reales finitos.
- En los conjuntos no acotados, los extremos se describen mediante los símbolos más o menos infinito (±∞).
Un conjunto puede estar acotado superiormente, con un extremo superior finito, y no estar acotado inferiormente, con un extremo inferior infinito, o darse exactamente la situación contraria.
Nota. Los extremos de un conjunto pueden pertenecer o no al propio conjunto.
Para afianzar estos conceptos, conviene analizar por separado el extremo inferior y el extremo superior a través de ejemplos claros y representativos.
Extremo inferior (ínfimo)
Sea \( A \subseteq \mathbb{R} \) un conjunto y sea B un subconjunto no vacío $$ B \subseteq A $$ El extremo inferior, o ínfimo, de B es el número real \( a \) tal que $$ a \le b \:\:\: \forall \, b \in B $$ y con la propiedad de que cualquier número real estrictamente mayor que \( a \) deja de ser una cota inferior de B. $$ inf(B) = a $$
Dicho de otro modo, el extremo inferior es la mayor de todas las cotas inferiores del conjunto B.
El ínfimo puede pertenecer o no al conjunto. Cuando pertenece al conjunto, se denomina mínimo.
Por ejemplo, el extremo inferior de B es el número 3.
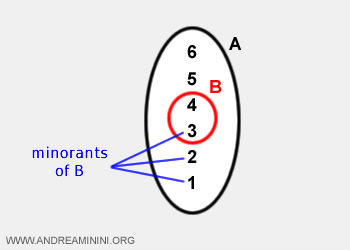
En los conjuntos acotados, el extremo inferior es un número real finito y coincide con el máximo del conjunto de todas las cotas inferiores (minorantes).
En cambio, si un conjunto no está acotado inferiormente, su extremo inferior es menos infinito (-∞).
Ejemplo 1
Sea A el conjunto de todos los números reales \( \mathbb{R} \).
Sea B un subconjunto de A formado por siete números reales:
$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$
El extremo inferior del conjunto B es el número tres.
$$ inf(B) = 3 \le b \:\:\: \forall \, b \in B $$
Esto se debe a que 3 es menor o igual que todos los elementos de B.
Nota. En este caso, el extremo inferior \( inf(B)=3 \) pertenece al conjunto B, pero esto no ocurre necesariamente en todos los conjuntos.
Ejemplo 2
Sea A el conjunto de todos los números reales \( \mathbb{R} \).
Sea B el conjunto de los números reales positivos \( \mathbb{R}^+ \).
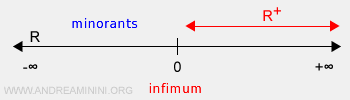
El extremo inferior del conjunto B es cero.
$$ inf(B) \le b \:\:\: \forall \, b \in B $$
Este valor es la mayor de todas las cotas inferiores del conjunto \( \mathbb{R}^+ \).
Nota. En este caso, el extremo inferior \( inf(B)=0 \) no pertenece al conjunto B, ya que entre cero y cualquier número real positivo existen infinitos puntos intermedios.
Extremo superior (supremo)
Sea \( A \subseteq \mathbb{R} \) un conjunto y sea B un subconjunto no vacío $$ B \subseteq A $$ El extremo superior, o supremo, de B es el número real \( a \) tal que $$ a \ge b \:\:\: \forall \, b \in B $$ y con la propiedad de que cualquier número real estrictamente menor que \( a \) deja de ser una cota superior de B. $$ sup(B) = a $$
De forma equivalente, el extremo superior es la menor de todas las cotas superiores del conjunto B.
El supremo puede pertenecer o no al conjunto. Cuando pertenece al conjunto, se denomina máximo.
Por ejemplo, el extremo superior de B es 4.
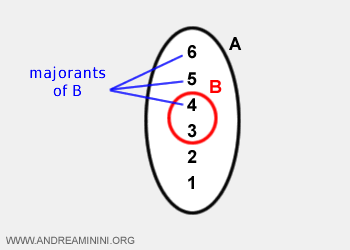
En los conjuntos acotados, el extremo superior es un número real finito y coincide con el mínimo del conjunto de todas las cotas superiores (mayorantes).
Si el conjunto no está acotado superiormente, su extremo superior es más infinito (+∞).
Ejemplo 1
Sea A el conjunto de todos los números reales \( \mathbb{R} \).
Sea B el siguiente subconjunto de A:
$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$
El extremo superior del conjunto B es el número nueve.
$$ sup(B) = 9 \ge b \:\:\: \forall \, b \in B $$
Esto se debe a que 9 es mayor o igual que todos los elementos del conjunto.
Nota. En este ejemplo, el extremo superior \( sup(B)=9 \) pertenece al conjunto B, pero esto no es una regla general.
Ejemplo 2
Sea A el conjunto de todos los números reales \( \mathbb{R} \).
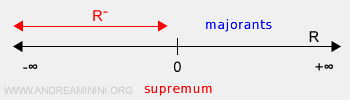
Sea B el conjunto de los números reales negativos \( \mathbb{R}^- \).
El extremo inferior del conjunto B es menos infinito.
$$ inf(B) = -\infty \le b \:\:\: \forall \, b \in B $$
Nota. En este caso, el extremo inferior pertenece a la recta real extendida, pero no al conjunto B, que no está acotado inferiormente. Por otro lado, el extremo superior \( sup(B)=0 \) no pertenece al conjunto, ya que cero no es un número real negativo.
Extremos de un conjunto real
Los extremos inferior y superior de un conjunto real también pueden caracterizarse mediante condiciones equivalentes, especialmente útiles en análisis matemático.
Extremo inferior de un conjunto real
Sea \( E \subset \mathbb{R} \) un conjunto acotado inferiormente. El extremo inferior de \( E \) es el número real \( m \) tal que:
- para todo \( x \in E \), se cumple \( x \ge m \);
- para todo \( \varepsilon > 0 \), existe al menos un elemento \( x \in E \) tal que \( x < m + \varepsilon \).
En este caso, se escribe \( m = \inf E \).
Esta formulación expresa que \( m \) es la mayor de todas las cotas inferiores del conjunto \( E \).
Extremo superior de un conjunto real
Sea \( E \subset \mathbb{R} \) un conjunto acotado superiormente. El extremo superior de \( E \) es el número real \( M \) tal que:
- para todo \( x \in E \), se cumple \( x \le M \);
- para todo \( \varepsilon > 0 \), existe al menos un elemento \( x \in E \) tal que \( x > M - \varepsilon \).
En este caso, se escribe \( M = \sup E \).
Esta formulación expresa que \( M \) es la menor de todas las cotas superiores del conjunto \( E \).
Notas
Comentarios y observaciones finales
- Todo subconjunto no vacío de los números reales admite un extremo inferior y un extremo superior
En particular, si un conjunto no está acotado superiormente, su extremo superior es \( \sup A = +\infty \). De manera análoga, si no está acotado inferiormente, su extremo inferior es \( \inf A = -\infty \). Cuando un conjunto está acotado, los extremos finitos existen y son únicos. Por ello, la noción de extremo está siempre bien definida dentro del marco de los números reales extendidos.Por “números reales extendidos” se entiende la recta real \( \mathbb{R} \) ampliada con los símbolos \( -\infty \) y \( +\infty \). Estos símbolos no son números reales, pero se introducen para garantizar que los extremos inferior y superior estén siempre definidos.
Y así sucesivamente.