Subconjuntos
Un conjunto A es un subconjunto de B si cada elemento de A también pertenece a B.
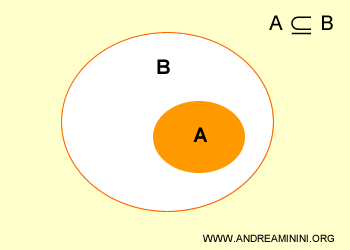
La representación gráfica de los conjuntos mostrada arriba se conoce como un diagrama de Venn.
En otras palabras, el subconjunto A está contenido en el conjunto B.
Esta relación se denomina inclusión.
Para expresar la inclusión normal, se utiliza el símbolo ⊆.
Se lee como "el conjunto A está contenido en el conjunto B".
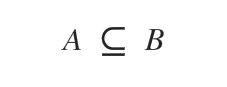
Otras formas de interpretar esta notación son "A es un subconjunto de B" o "A está incluido en B".
La relación de inclusión también se puede expresar de la siguiente manera:
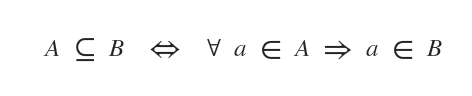
Nota. La relación de inclusión también incluye el caso en el que A y B son conjuntos idénticos, es decir, tienen exactamente los mismos elementos. De hecho, el símbolo es una combinación del símbolo de inclusión (⊂) y el símbolo de igualdad (=).
El Subconjunto Propio
Un subconjunto propio se refiere al caso en el que el subconjunto A está contenido en el conjunto B, pero hay al menos un elemento en B que no está en A.
En pocas palabras, los dos conjuntos son distintos, es decir, A≠B.
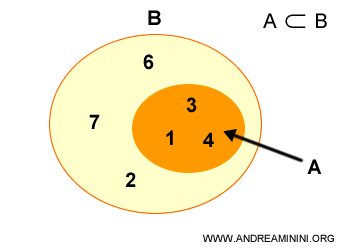
A esta situación se le llama inclusión estricta.
Es un tipo específico de inclusión, representado por el símbolo ⊂.
Significa que "el conjunto A es una parte propia de B".
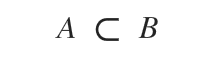
También se puede decir que "el conjunto A está estrictamente incluido en el conjunto B".
Ejemplo
El conjunto A está estrictamente incluido en el conjunto B
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4,2,6,7 \} $$
Porque cada elemento de A también es un elemento de B, pero B contiene elementos que no están en A.
$$ A ⊂ B $$
¿Cuál es la diferencia entre inclusión normal e inclusión estricta? En la inclusión estricta (A⊂B), los conjuntos A y B son siempre diferentes (A≠B). En la inclusión normal (A⊆B), en cambio, los dos conjuntos pueden ser idénticos (A=B). Por lo tanto, si la inclusión estricta (A⊂B) es verdadera, también lo es la inclusión normal (A⊆B). $$ A⊂B \Longrightarrow A⊆B $$ Por el contrario, si la inclusión normal (A⊆B) es verdadera, esto no implica necesariamente que la inclusión estricta (A⊂B) también lo sea, ya que los conjuntos podrían ser idénticos (A=B).
El Subconjunto Impropio
- Todo conjunto tiene siempre dos subconjuntos impropios:
- un conjunto idéntico a sí mismo
- el conjunto vacío
A] El conjunto idéntico a sí mismo
Cuando dos conjuntos son iguales (A=B), cada conjunto es un subconjunto del otro.
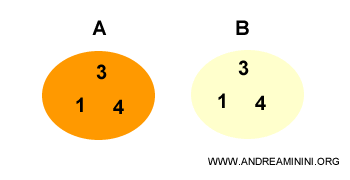
Porque A contiene todos los elementos de B y B contiene todos los elementos de A.
En este caso, se dice que:
- A es un subconjunto impropio de B
- B es un subconjunto impropio de A
Esta relación particular de implicación mutua implica la igualdad entre los conjuntos.
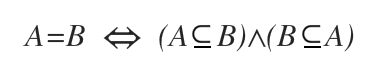
Por lo tanto, cuando dos conjuntos son iguales, también son subconjuntos impropios uno del otro.
Ejemplo
El conjunto A está incluido en el conjunto B y viceversa
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4 \} $$
Porque cada elemento del conjunto A también es un elemento de B y cada elemento de B también es un elemento de A.
Así, los dos conjuntos son iguales (A=B).
B] El conjunto vacío
El conjunto vacío se considera un subconjunto impropio de cualquier conjunto.
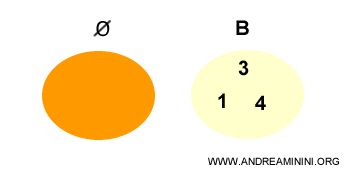
Un conjunto vacío se define como un conjunto que no tiene elementos.
Se representa con el símbolo Ø. $$ Ø = \{ \ \ \} $$
Nota. La idea de que el conjunto vacío se considere subconjunto de todos los demás conjuntos puede parecer al principio difícil de entender, pero se puede demostrar (ver demostración).
Ejemplo
Considera el conjunto vacío y cualquier conjunto A.
$$ Ø = \{ \ \ \} $$
$$ A = \{ 1,3,4 \} $$
El conjunto vacío Ø también está estrictamente incluido en A
$$ Ø ⊂ A $$
Porque no se puede afirmar lo contrario.
Demostración. La demostración se realiza por contradicción, suponiendo lo contrario. Si el conjunto vacío NO fuera un subconjunto de A, entonces tendría que haber al menos un elemento en el conjunto vacío que no esté en A. Sin embargo, esto es imposible porque el conjunto vacío no tiene elementos. Por lo tanto, si la afirmación "el conjunto vacío no es un subconjunto de A" es falsa, entonces la afirmación opuesta "el conjunto vacío es un subconjunto de A" es verdadera. Demostración alternativa. La unión de un conjunto A con uno de sus subconjuntos B⊆A es siempre igual al conjunto en sí. $$ A \cup B = A $$ Lo mismo ocurre con la unión de un conjunto y el conjunto vacío $$ A \cup Ø = \{ 1,3,4 \} \cup \{ \ \ \} = \{ 1,3,4 \} = A $$
El Singleton
¿Qué es un singleton?
Un singleton es un subconjunto que contiene solo un elemento.
Ejemplo
El subconjunto B es un singleton porque es un subconjunto ( B⊂A ) y contiene solo un elemento.
$$ A = \{ 1, 2, 3, 4, 5\} $$
$$ B = \{ 2 \} $$
La Diferencia Entre Inclusión y Pertenencia
Es importante no confundir los conceptos de inclusión y pertenencia.
- La relación de inclusión ⊆ se usa exclusivamente entre conjuntos. Se aplica para indicar que el conjunto A es un subconjunto de B. $$ A \subseteq B $$
- La relación de pertenencia ∈ se emplea únicamente entre elementos y un conjunto. Sirve para indicar que uno o más elementos, como a, b, pertenecen al conjunto A. $$ a \in A $$
Nota: El mismo principio se aplica a las relaciones de no inclusión y no pertenencia (∉). $$ a \notin A \\ A \nsubseteq B $$