La Diferencia Simétrica entre Conjuntos

La diferencia simétrica entre dos conjuntos A y B es el conjunto de elementos que pertenecen a uno de los conjuntos, pero no a ambos al mismo tiempo. Se expresa de la siguiente manera: $$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Esta operación permite identificar los elementos exclusivos de cada conjunto, descartando aquellos que son comunes a ambos.

Formalmente, se define así:

$$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Donde:

• A\B es el conjunto de elementos que están en A pero no en B.
• B\A es el conjunto de elementos que están en B pero no en A.

En otras palabras, la diferencia simétrica es la unión de los elementos que pertenecen exclusivamente a cada conjunto.

Esta operación es especialmente útil para resaltar las diferencias entre dos conjuntos.

En un diagrama de Venn, la diferencia simétrica se representa con las áreas que no se superponen entre los dos círculos que representan los conjuntos.

Un Ejemplo Práctico

Supongamos que tenemos los siguientes conjuntos A y B:

$$ A = \{1, 2, 3\} $$

$$ B = \{2, 3, 4\} $$

Para encontrar la diferencia simétrica \(A \Delta B\), identificamos los elementos que están en A pero no en B, y viceversa:

$$ A \setminus B = \{1\} $$

$$ B \setminus A = \{4\} $$

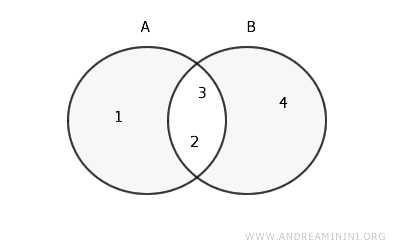
Por lo tanto, la diferencia simétrica entre A y B es el conjunto {1, 4}.

$$ A \Delta B = \{1\} \cup \{4\} = \{1, 4\} $$

En un diagrama de Venn, se vería así:

Ejemplo 2

Veamos otro caso:

$$ A = \{a, b, c\} $$

$$ B = \{c, d, e\} $$

Aplicamos el mismo procedimiento:

$$ A \setminus B = \{a, b\} $$

$$ B \setminus A = \{d, e\} $$

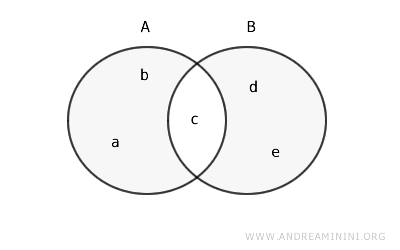
Por lo tanto, la diferencia simétrica entre A y B es el conjunto {a, b, d, e}.

$$ A \Delta B = \{a, b\} \cup \{d, e\} = \{a, b, d, e\} $$

En un diagrama de Venn, se representa de la siguiente manera:

Propiedades de la Diferencia Simétrica

La diferencia simétrica tiene varias propiedades interesantes:

• Conmutatividad
  El orden de los conjuntos no afecta el resultado: \[ A \Delta B = B \Delta A \]
• Asociatividad
  Se pueden agrupar los conjuntos de distintas formas sin alterar el resultado: \[ A \Delta (B \Delta C) = (A \Delta B) \Delta C \]
• Elemento Neutro
  La diferencia simétrica de un conjunto con el conjunto vacío es el mismo conjunto: \[ A \Delta \emptyset = A \]
• Idempotencia
  La diferencia simétrica de un conjunto consigo mismo es el conjunto vacío: \[ A \Delta A = \emptyset \]

Estas propiedades hacen que la diferencia simétrica sea una herramienta útil en distintos contextos matemáticos.